题目内容
已知△ABC的面积为1，在△ABC所在的平面内有两点P、Q，满足
+
=
，
+
+
=
，则四边形BCPQ的面积为______．
| PA |
| PC |
| 0 |
| QA |
| QB |
| QC |
| BC |
∵点P满足
+
=
，
∴
=-
，可得点P是线段AC的中点
又∵
+
+
=
∴
=
+
+
=2
可得Q是线段AB的靠近B点的三等分点
因此，△APQ的面积为
S△APQ=
|
|•|
|sinA=
•
|
|•
|
|=
S△ABC
∵△ABC的面积为1，∴S△APQ=
由此可得四边形BCPQ的面积为S=S△ABC-S△APQ=1-
=
故答案为：
| PA |
| PC |
| 0 |
∴
| PA |
| PC |
又∵
| QA |
| QB |
| QC |
| BC |
∴
| QA |
| BC |
| CQ |
| BQ |
| BQ |
可得Q是线段AB的靠近B点的三等分点
因此，△APQ的面积为
S△APQ=
| 1 |
| 2 |
| AP |
| AQ |
| 1 |
| 2 |
| 1 |
| 2 |
| AC |
| 2 |
| 3 |
| AB |
| 1 |
| 3 |
∵△ABC的面积为1，∴S△APQ=
| 1 |
| 3 |
由此可得四边形BCPQ的面积为S=S△ABC-S△APQ=1-
| 1 |
| 3 |
| 2 |
| 3 |
故答案为：
| 2 |
| 3 |
练习册系列答案
相关题目
，
，
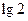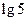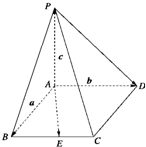
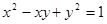有以下判断：（1）它表示圆；（2）它关于原点对称；（3）它关于直线
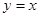对称；（4）
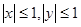．其中正确的有________（填上相应的序号即可）.
，
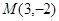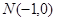，则线段
的中点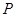
的坐标是________.
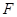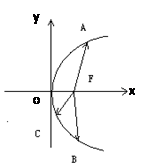
为抛物线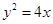
的焦点，A、B、C在抛物线上，若
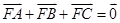，则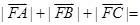
（ ）
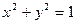上等可能的任取一点A，以OA（O为坐标原点）为终边的角为
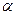，则使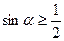
的概率为（ ）
