Question

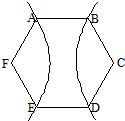如图，已知ABCDEF为正六边形，若以C，F为焦点的双曲线恰好经过A，B，D，E四点，则该双曲线的离心率为

 

．

Answer 1

分析：正六边形ABCDEF的边长为2，以FC为x轴，以FC的垂直平分线为y轴建立平面直角坐标系，根据题设条件能够求出双曲线的实半轴a和半焦距c，由此能够求出该双曲线的离心率．

解答：解：设正六边形ABCDEF的边长为2，以FC为x轴，以FC的垂直平分线为y轴建立平面直角坐标系，
由题意可知，B（1，

3

），F（-2，0），C（2，0），c=2．
∴|BF|=

(1+2)2+( 3 -0)2

=2

3

，|BC|=

(1-2)2+( 3 -0)2

=2，
∴2a=|BF|-|BC|=2

3

-2，
∴a=

3

-1
∴e=

c

a

=

2

3 -1

=

3

+1．
答案：

3

+1．

点评：恰当地选取平面直角坐标系，能够简化运算．