题目内容
 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.(Ⅰ)求证:AF⊥平面CDE;
(Ⅱ)求面ACD和面BCE所成锐二面角的大小.
分析:(Ⅰ)利用等腰三角形的性质、线面垂直的判定和性质定理即可证明;
(Ⅱ)建立如图所示的空间直角坐标系,利用两个平面的法向量所成的夹角即可得出二面角的大小.
(Ⅱ)建立如图所示的空间直角坐标系,利用两个平面的法向量所成的夹角即可得出二面角的大小.
解答:(Ⅰ)证明:∵DE⊥平面ACD,AF?平面ACD,∴DE⊥AF.
又∵AC=AD,F为CD的中点,∴AF⊥CD.
又∵CD∩DE=D,AF⊥平面CDE.
(Ⅱ)由(Ⅰ)可知:平面ACD⊥平面CDE.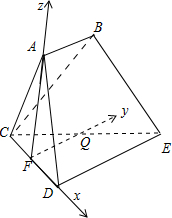
取CE的中点Q,连接FQ,∴FQ∥DE,
∴FQ⊥平面ACD.于是可得FD,FQ,FA两两垂直,以F为坐标原点,建立如图所示的空间直角坐标系.
则F(0,0,0),C(-1,0,0),A(0,0,
),B(0,1,
),E(1,2,0).
∴
=(1,1,
),
=(2,2,0),
设平面BCE的法向量
=(x,y,z),则
,化为
,
令x=1,则y=-1,z=0,∴
=(1,-1,0),
∵FQ⊥平面ACD,于是可取平面ACD的法向量为
=(0,1,0).
.
∴|cos<
,
>|=
=
=
.
∴平面ACD和平面BCE所成锐二面角为45°.
又∵AC=AD,F为CD的中点,∴AF⊥CD.
又∵CD∩DE=D,AF⊥平面CDE.
(Ⅱ)由(Ⅰ)可知:平面ACD⊥平面CDE.

取CE的中点Q,连接FQ,∴FQ∥DE,
∴FQ⊥平面ACD.于是可得FD,FQ,FA两两垂直,以F为坐标原点,建立如图所示的空间直角坐标系.
则F(0,0,0),C(-1,0,0),A(0,0,
| 3 |
| 3 |
∴
| CB |
| 3 |
| CE |
设平面BCE的法向量
| n |
|
|
令x=1,则y=-1,z=0,∴
| n |
∵FQ⊥平面ACD,于是可取平面ACD的法向量为
| FQ |
.
∴|cos<
| n |
| FQ |
|
| ||||
|
|
| 1 | ||
|
| ||
| 2 |
∴平面ACD和平面BCE所成锐二面角为45°.
点评:熟练掌握等腰三角形的性质、面面、线面垂直的判定和性质定理、通过建立空间直角坐标系并利用两个平面的法向量所成的夹角求二面角的方法是解题的关键.

练习册系列答案
相关题目
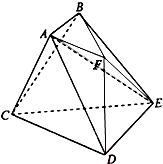 如图,已知多面体ABCDEF中,AB⊥平面ACDF,DE⊥平面ACDF,△ACD是正三角形,且
如图,已知多面体ABCDEF中,AB⊥平面ACDF,DE⊥平面ACDF,△ACD是正三角形,且 如图,已知多面体ABCDE中,DE⊥平面DBC,DE∥AB,BD=CD=BC=AB=2,F为BC的中点.
如图,已知多面体ABCDE中,DE⊥平面DBC,DE∥AB,BD=CD=BC=AB=2,F为BC的中点. 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1. 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.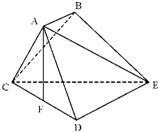 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.