题目内容
 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.( I)求证:求证AF⊥CD;
(II)求多面体ABCDE的体积.
分析:( I)取CD的中点O,连接AO、OF,则OF∥DE,利用线面垂直的判断性质得到DE⊥CD,OF⊥CD,利用线面垂直的判断得到CD⊥平面AOF,AF?平面AOF得到AF⊥CD.
(II)取AD中点G,根据AC=AD=CD=2,可得CG⊥AD,CG=
,利用平面ABED⊥平面ACD,可知CG⊥平面ABED,从而可求多面体ABCDE的体积.
(II)取AD中点G,根据AC=AD=CD=2,可得CG⊥AD,CG=
| 3 |
解答: 解:( I)取CD的中点O,连接AO、OF,则OF∥DE,
解:( I)取CD的中点O,连接AO、OF,则OF∥DE,
∵AC=AD,
∴AO⊥CD
∵DE⊥平面ACD
∴DE⊥CD
∴OF⊥CD,
又AO∩OF=O
∴CD⊥平面AOF
∵AF?平面AOF
∴AF⊥CD.
(II)取AD中点G,
∵AC=AD=CD=2,
∴CG⊥AD,CG=
∵AB⊥平面ACD,DE⊥平面ACD
∴平面ABED⊥平面ACD
∴CG⊥平面ABED
∵DE=2,AB=1
∴VABCDE=
SABED•CG=
•
(AB+DE)•AD•
=
.
 解:( I)取CD的中点O,连接AO、OF,则OF∥DE,
解:( I)取CD的中点O,连接AO、OF,则OF∥DE,∵AC=AD,
∴AO⊥CD
∵DE⊥平面ACD
∴DE⊥CD
∴OF⊥CD,
又AO∩OF=O
∴CD⊥平面AOF
∵AF?平面AOF
∴AF⊥CD.
(II)取AD中点G,
∵AC=AD=CD=2,
∴CG⊥AD,CG=
| 3 |
∵AB⊥平面ACD,DE⊥平面ACD
∴平面ABED⊥平面ACD
∴CG⊥平面ABED
∵DE=2,AB=1
∴VABCDE=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
点评:本题以多面体为载体,考查线面垂直,考查线线垂直,考查几何体的体积,解答的关键是正确运用线面垂直的判定定理.

练习册系列答案
相关题目
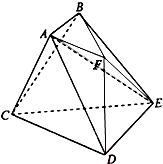 如图,已知多面体ABCDEF中,AB⊥平面ACDF,DE⊥平面ACDF,△ACD是正三角形,且
如图,已知多面体ABCDEF中,AB⊥平面ACDF,DE⊥平面ACDF,△ACD是正三角形,且 如图,已知多面体ABCDE中,DE⊥平面DBC,DE∥AB,BD=CD=BC=AB=2,F为BC的中点.
如图,已知多面体ABCDE中,DE⊥平面DBC,DE∥AB,BD=CD=BC=AB=2,F为BC的中点. 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1.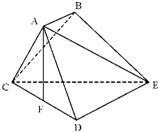 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.