题目内容
 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1.(1)求直线AE与平面CDE所成角的大小(用反三角函数值表示);
(2)求多面体ABCDE的体积.
分析:(1)要求线面角,必需找到该斜线与其射影的夹角,即要证明线面垂直,进而得到垂线、斜线与斜线的射影,即可根据解三角形的有关知识解决问题.
(2)结合(1)中的证明思路可得:线面垂直即CN⊥平面ABED,再利用棱锥的体积公式,进而求出四棱锥的体积;
(2)结合(1)中的证明思路可得:线面垂直即CN⊥平面ABED,再利用棱锥的体积公式,进而求出四棱锥的体积;
解答:解:(1)取CD中点M,连接AM与EM (1分)
∵△ACD是正三角形,
∴AM⊥CD.(2分)
∵DE⊥平面ACD,
∴DE⊥AM.(3分)
又CD∩DE=D,
∴AM⊥平面CDE.(4分)
所以∠AEM就是AE与平面CDE所成角 (5分)
根据题意可得:在△AME中,AM=
,EM=
,
∴tan∠AEM=
.(7分)
所以直线AE与平面CDE所成角的大小为arctan
(写成arcsin
或arccos
也可).(8分)
(2)取AD中点N,同理(1)可证CN⊥平面ABED,且CN=
.(10分)
由题意可得:VABCDE=VC-ABED=
SABED•CN=
•
•AD•CN=
•
•2•
=
.(14分)
∵△ACD是正三角形,
∴AM⊥CD.(2分)
∵DE⊥平面ACD,
∴DE⊥AM.(3分)
又CD∩DE=D,
∴AM⊥平面CDE.(4分)
所以∠AEM就是AE与平面CDE所成角 (5分)
根据题意可得:在△AME中,AM=
| 3 |
| 5 |
∴tan∠AEM=
| ||
| 5 |
所以直线AE与平面CDE所成角的大小为arctan
| ||
| 5 |
| ||
| 4 |
| ||
| 4 |
(2)取AD中点N,同理(1)可证CN⊥平面ABED,且CN=
| 3 |
由题意可得:VABCDE=VC-ABED=
| 1 |
| 3 |
| 1 |
| 3 |
| AB+DE |
| 2 |
| 1 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
点评:本题主要考查线面垂直的判定定理与几何体体积的求解,以及线面角,而解决空间角的步骤是:找角,证角,求角三步,空间角是高考比考内容.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
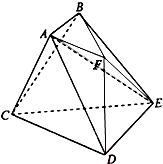 如图,已知多面体ABCDEF中,AB⊥平面ACDF,DE⊥平面ACDF,△ACD是正三角形,且
如图,已知多面体ABCDEF中,AB⊥平面ACDF,DE⊥平面ACDF,△ACD是正三角形,且 如图,已知多面体ABCDE中,DE⊥平面DBC,DE∥AB,BD=CD=BC=AB=2,F为BC的中点.
如图,已知多面体ABCDE中,DE⊥平面DBC,DE∥AB,BD=CD=BC=AB=2,F为BC的中点. 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.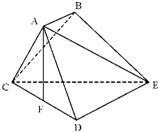 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.