题目内容
 如图,已知多面体ABCDE中,AE⊥平面ABC,AE
如图,已知多面体ABCDE中,AE⊥平面ABC,AE
| ||
. |
| 1 |
| 2 |
(Ⅰ)求证:平面BDE⊥平面BCD;
(Ⅱ)求平面ABE与平面BCD所成的锐二面角的大小.
分析:(Ⅰ)取BC、BD的中点M、N,连接AM、EN和MN,则MN
CD.由AE
CD,知MN
AE,由AE⊥平面ABC,知AE⊥AM,所以ABMN为矩形,NE⊥MN.由此入手能够证明面BCE⊥面CDE.
(Ⅱ)过C作直线l∥AB,则l∥DE,所以面ABC∩面EDC=l.由AB⊥平面ACD,知l⊥面ACD,所以∠ACD即为所求二面角的平面角,由此能求出其结果.
| ||
. |
| 1 |
| 2 |
| ||
. |
| 1 |
| 2 |
| ||
. |
(Ⅱ)过C作直线l∥AB,则l∥DE,所以面ABC∩面EDC=l.由AB⊥平面ACD,知l⊥面ACD,所以∠ACD即为所求二面角的平面角,由此能求出其结果.
解答: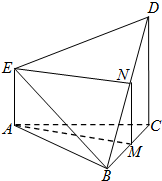 (Ⅰ)证明:取BC、BD的中点M、N,连接AM、EN和MN,
(Ⅰ)证明:取BC、BD的中点M、N,连接AM、EN和MN,
则MN
CD.
∵AE
CD,∴MN
AE,
又AE⊥平面ABC,AM⊆面ABC,∴AE⊥AM,
∴ABMN为矩形,∴NE⊥MN.
∵AB⊥平面ACD,DE∥AB,∴DE⊥平面ACD,
∵△ACD为正三角形,N为CD的中点,
∴AN⊥CD,又面CDE∩面ACD=CD,
∴AN⊥面CDE,∴CM⊥面CDE,∴面BCE⊥面CDE;
(Ⅱ)解:过C作直线l∥AB,则l∥DE,
∴面ABC∩面EDC=l.
∵AB⊥平面ACD,∴l⊥面ACD,
∴∠ACD即为所求二面角的平面角,为600.
 (Ⅰ)证明:取BC、BD的中点M、N,连接AM、EN和MN,
(Ⅰ)证明:取BC、BD的中点M、N,连接AM、EN和MN,则MN
| ||
. |
| 1 |
| 2 |
∵AE
| ||
. |
| 1 |
| 2 |
| ||
. |
又AE⊥平面ABC,AM⊆面ABC,∴AE⊥AM,
∴ABMN为矩形,∴NE⊥MN.
∵AB⊥平面ACD,DE∥AB,∴DE⊥平面ACD,
∵△ACD为正三角形,N为CD的中点,
∴AN⊥CD,又面CDE∩面ACD=CD,
∴AN⊥面CDE,∴CM⊥面CDE,∴面BCE⊥面CDE;
(Ⅱ)解:过C作直线l∥AB,则l∥DE,
∴面ABC∩面EDC=l.
∵AB⊥平面ACD,∴l⊥面ACD,
∴∠ACD即为所求二面角的平面角,为600.
点评:本题考查平面与平面垂直的证明和求二面角的大小,解题时要认真审题,注意把空间几何问题等价转化为平面几何问题.

练习册系列答案
相关题目
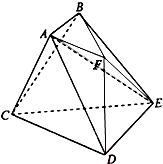 如图,已知多面体ABCDEF中,AB⊥平面ACDF,DE⊥平面ACDF,△ACD是正三角形,且
如图,已知多面体ABCDEF中,AB⊥平面ACDF,DE⊥平面ACDF,△ACD是正三角形,且 如图,已知多面体ABCDE中,DE⊥平面DBC,DE∥AB,BD=CD=BC=AB=2,F为BC的中点.
如图,已知多面体ABCDE中,DE⊥平面DBC,DE∥AB,BD=CD=BC=AB=2,F为BC的中点. 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1. 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.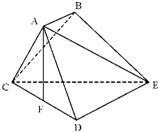 如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.
如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.