Question

【题目】如图，四棱锥的底面是平行四边形， 平面， ，点是棱上异于、的一点.

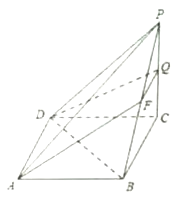
（1）求证： ；

（2）过点和平面截四棱锥得到截面（点在棱上），求证： .

Answer 1

【答案】(1)证明见解析；(2)证明见解析.

【解析】试题分析：（1）先利用面面垂直的性质和等腰三角形的“三线合一”得到线线垂直，再利用线面垂直的判定定理证明线面垂直，进而得到线线垂直；（2）先利用线面平行的判定定理证明线面平行，再利用线面平行的性质定理进行证明.

试题解析：（1）证明： 平面， 平面，所以，记， 交于点，平行四边形对角线互相平分，则为的中点，又中， ，

所以，又， ， 平面，所以平面，又平面

所以；

（2）四边形是平行四边形，所以，又平面， 平面，所以平面，又 平面，平面 平面，所以，又，所以.