题目内容
【题目】已知函数![]() 的两个极值点分别在(-1,0)与(0,1)内,则2a-b的取值范围是( )
的两个极值点分别在(-1,0)与(0,1)内,则2a-b的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
求出导函数f′(x)=3x2+4ax+3b,由3x2+4ax+3b=0的两个根分别在区间(0,1)与(﹣1,0)内,列出约束条件,利用线性规划求解2a﹣b的取值范围.
由函数f(x)=x3+2ax2+3bx+c,求导f′(x)=3x2+4ax+3b,
f(x)的两个极值点分别在区间(﹣1,0)与(0,1)内,
由3x2+4ax+3b=0的两个根分别在区间(0,1)与(﹣1,0)内,
即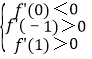 ,令z=2a﹣b,
,令z=2a﹣b,
∴转化为在约束条件为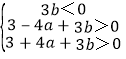 时,求z=2a﹣b的取值范围,可行域如下阴影(不包括边界),
时,求z=2a﹣b的取值范围,可行域如下阴影(不包括边界),
目标函数转化为z=2a﹣b,由图可知,z在A(![]() ,0)处取得最大值
,0)处取得最大值![]() ,在(
,在(![]() ,0)处取得最小值
,0)处取得最小值![]() ,
,
因为可行域不包含边界,∴z=2a﹣b的取值范围(![]() ,
,![]() ).
).
故选:B.

练习册系列答案
相关题目