题目内容
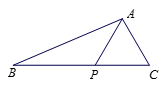
【题目】已知△ABC内一点O满足 ![]() =
= ![]() ,若△ABC内任意投一个点,则该点△OAC内的概率为( )
,若△ABC内任意投一个点,则该点△OAC内的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:以 ![]() ,
, ![]() 为邻边作平行四边形OBDC,则
为邻边作平行四边形OBDC,则 ![]() +
+ ![]() =
= ![]() ∵
∵ ![]() =
= ![]() ,
,
∴3 ![]() =
= ![]() ,
,
作AB的两个三等分点E,F,则 ![]() =
= ![]() =
= ![]() ,
,
∴O到AC的距离是E到AC距离的一半,B到AC的距离是O到AC距离的3倍,如图
∴S△AOC= ![]() S△ABC .
S△ABC .
故△ABC内任意投一个点,则该点△OAC内的概率为 ![]() ,
,
故选:C.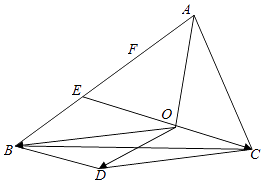
要求该概率即求S△AOC:S△ABC=的比值.由 ![]() =
= ![]() ,变形为:3
,变形为:3 ![]() =
= ![]() ,得到O到AC的距离是E到AC距离的一半,B到AC的距离是O到AC距离的3倍,两三角形同底,面积之比转化为概率.
,得到O到AC的距离是E到AC距离的一半,B到AC的距离是O到AC距离的3倍,两三角形同底,面积之比转化为概率.

练习册系列答案
相关题目
【题目】某公司对新研发的一种产品进行合理定价,且销量与单价具有相关关系,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x(单位:元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y(单位:万件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)现有三条y对x的回归直线方程: ![]() =﹣10x+170;
=﹣10x+170; ![]() =﹣20x+250;
=﹣20x+250; ![]() =﹣15x+210;根据所学的统计学知识,选择一条合理的回归直线,并说明理由.
=﹣15x+210;根据所学的统计学知识,选择一条合理的回归直线,并说明理由.
(2)预计在今后的销售中,销量与单价服从(1)中选出的回归直线方程,且该产品的成本是每件5元,为使公司获得最大利润,该产品的单价应定多少元?(利润=销售收入﹣成本)