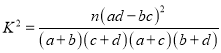题目内容
【题目】已知函数![]() (
(![]() ,
, ![]() ),且对任意
),且对任意![]() ,都有
,都有![]() .
.
(Ⅰ)用含![]() 的表达式表示
的表达式表示![]() ;
;
(Ⅱ)若![]() 存在两个极值点
存在两个极值点![]() ,
, ![]() ,且
,且![]() ,求出
,求出![]() 的取值范围,并证明
的取值范围,并证明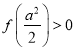 ;
;
(Ⅲ)在(Ⅱ)的条件下,判断![]() 零点的个数,并说明理由.
零点的个数,并说明理由.
【答案】(1)![]() (2)见解析(3)见解析
(2)见解析(3)见解析
【解析】试题分析:利用赋值法求出![]() 关系,求函数导数,要求函数有两个极值点,只需
关系,求函数导数,要求函数有两个极值点,只需![]() 在
在![]() 内有两个实根,利用一元二次方程的根的分布求出
内有两个实根,利用一元二次方程的根的分布求出![]() 的取值范围,再根据函数图象和极值的大小判断零点的个数.
的取值范围,再根据函数图象和极值的大小判断零点的个数.
试题解析:(Ⅰ)根据题意:令![]() ,可得
,可得![]() ,
,
所以![]() ,
,
经验证,可得当![]() 时,对任意
时,对任意![]() ,都有
,都有![]() ,
,
所以![]() .
.
(Ⅱ)由(Ⅰ)可知![]() ,且
,且![]() ,
,
所以![]()
![]() ,
,
令![]() ,要使
,要使![]() 存在两个极值点
存在两个极值点![]() ,
, ![]() ,则须有
,则须有![]() 有两个不相等的正数根,所以
有两个不相等的正数根,所以
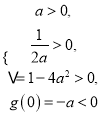 或
或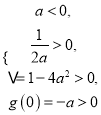
解得![]() 或无解,所以
或无解,所以![]() 的取值范围
的取值范围![]() ,可得
,可得![]() ,
,
由题意知 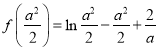
![]() ,
,
令![]()
![]() ,则
,则![]()
![]() .
.
而当![]() 时,
时, ![]()
![]() ,即
,即![]() ,
,
所以![]() 在
在![]() 上单调递减,
上单调递减,
所以
![]()
![]()
![]()
即![]() 时,
时, 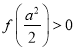 .
.
(Ⅲ)因为![]()
![]() ,
, ![]() .
.
令![]() 得
得![]() ,
, ![]() .
.
由(Ⅱ)知![]() 时,
时, ![]() 的对称轴
的对称轴![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() .
.
又![]() ,可得
,可得![]() ,此时,
,此时, ![]() 在
在![]() 上单调递减,
上单调递减, ![]() 上单调递增,
上单调递增, ![]() 上单调递减,所以
上单调递减,所以 ![]() 最多只有三个不同的零点.
最多只有三个不同的零点.
又因为![]() ,所以
,所以![]() 在
在![]() 上递增,即
上递增,即![]() 时,
时, ![]() 恒成立.
恒成立.
根据(2)可知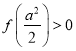 且
且![]() ,所以
,所以![]() ,即
,即![]() ,所以
,所以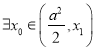 ,使得
,使得![]() .
.
由![]() ,得
,得![]() ,又
,又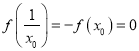 ,
, ![]() ,
,
所以![]() 恰有三个不同的零点:
恰有三个不同的零点: ![]() ,1,
,1, ![]() .
.
综上所述, ![]() 恰有三个不同的零点.
恰有三个不同的零点.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目