题目内容
17.二项式(x-$\frac{1}{x}$)8的展开式中x4的系数是( )| A. | 28 | B. | -28 | C. | 56 | D. | -56 |
分析 写出二项展开式的通项,由x的指数等于4求得r值,则答案可求.
解答 解:由${T}_{r+1}={C}_{8}^{r}{x}^{8-r}(-\frac{1}{x})^{r}=(-1)^{r}{C}_{8}^{r}{x}^{8-2r}$,
令8-2r=4,得r=2.
∴二项式(x-$\frac{1}{x}$)8的展开式中x4的系数是$(-1)^{2}{C}_{8}^{2}=28$.
故选:A.
点评 本题考查二项式系数的性质,关键是熟记二项展开式的通项及应用,是基础题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
7.城市公交车的数量若太多则容易造成资源的浪费;若太少又难以满足乘客需求.某市公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间作为样本分成5组,如下表所示(单位:分钟).
(I)估计这60名乘客中候车时间少于10分钟的人数;
(II)若从上表第三、四组的6人中任选2人作进一步的调查.
①列出所有可能的结果;
②求抽到的两人恰好来自不同组的概率.
| 组别 | 一 | 二 | 三 | 四 | 五 |
| 候车时间 | [0,5) | [5,10) | [10,15) | [15,20) | [20,25] |
| 人数 | 2 | 6 | 4 | 2 | l |
(II)若从上表第三、四组的6人中任选2人作进一步的调查.
①列出所有可能的结果;
②求抽到的两人恰好来自不同组的概率.
5.设O是△ABC的重心,且30sinA•$\overrightarrow{OA}$+42sinB•$\overrightarrow{OB}$+35sinC•$\overrightarrow{OC}$=$\overrightarrow{0}$,则sinB=( )
| A. | $\frac{5}{7}$ | B. | $\frac{6}{7}$ | C. | $\frac{2\sqrt{6}}{7}$ | D. | $\frac{\sqrt{13}}{7}$ |
12.某研究结构对高中学段学生的记忆能力x和识图能力y进行统计分析,得到如下数据:
若y与x的回归直线方程$\widehat{y}$=3x-$\frac{3}{2}$,则实数m的值是4.
| x | 0 | 1 | 2 | 3 |
| y | -1 | 1 | m | 8 |
2.某教师对全班50名学生的学习积极性和对待班级工作的态度进行了调查,得到如下2×2列联表:
(1)求2×2列联表中a1,a2,a3,a4的值,并用独立性检验的思想方法分析:是否有99.9%的把握认为“学生的学习积极性与对待班级工作的态度有关”?说明理由;
(2)随机抽查这个班的2名学生,求至少有1人积极参加班级工作的学生的概率.
附:
| 积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
| 学习积极性高 | 18 | a1 | 25 |
| 学习积极性一般 | a2 | 19 | a4 |
| 合计 | 24 | a3 | 50 |
(2)随机抽查这个班的2名学生,求至少有1人积极参加班级工作的学生的概率.
附:
| P(x2≥k) | 0.050 | 0.010 | 0.001 | x2=$\frac{n(ad-bc)^2}{(a+b)(c+d)(a+c)(b+d)}$ |
| k | 3.841 | 6.635 | 10.828 |
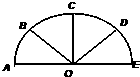 如图,在以AE=2为直径的半圆周上,B,C,D分别为弧AE的四等分点.
如图,在以AE=2为直径的半圆周上,B,C,D分别为弧AE的四等分点.