题目内容
5.设O是△ABC的重心,且30sinA•$\overrightarrow{OA}$+42sinB•$\overrightarrow{OB}$+35sinC•$\overrightarrow{OC}$=$\overrightarrow{0}$,则sinB=( )| A. | $\frac{5}{7}$ | B. | $\frac{6}{7}$ | C. | $\frac{2\sqrt{6}}{7}$ | D. | $\frac{\sqrt{13}}{7}$ |
分析 由O是△ABC的重心得:$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}$,则$\overrightarrow{OA}$=$-\overrightarrow{OB}-\overrightarrow{OC}$代入式子化简,利用向量相等列出方程组,化简后由正弦定理得到边之间的关系,由余弦定理求出cosB,根据平方关系和B的范围求出sinB的值.
解答 解:∵O是△ABC的重心,∴$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}$,则$\overrightarrow{OA}$=$-\overrightarrow{OB}-\overrightarrow{OC}$,
∵30sinA•$\overrightarrow{OA}$+42sinB•$\overrightarrow{OB}$+35sinC•$\overrightarrow{OC}$=$\overrightarrow{0}$,
∴30sinA•($-\overrightarrow{OB}-\overrightarrow{OC}$)+42sinB•$\overrightarrow{OB}$+35sinC•$\overrightarrow{OC}$=$\overrightarrow{0}$,
(42sinB-30sinA)•$\overrightarrow{OB}$+(35sinC-30sinA)•$\overrightarrow{OC}$=$\overrightarrow{0}$,
∵$\overrightarrow{OB}$与$\overrightarrow{OC}$不共线,∴$\left\{\begin{array}{l}{42sinB-30sinA=0}\\{35sinC-30sinA=0}\end{array}\right.$,
可得sinA=$\frac{7}{5}$sinB=$\frac{7}{6}$sinC,
由正弦定理得,b=$\frac{5}{7}$a、c=$\frac{6}{7}$a,
由余弦定理得,cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{{a}^{2}+{(\frac{6}{7}a)}^{2}-{(\frac{5}{7}a)}^{2}}{2a×\frac{6}{7}a}$=$\frac{5}{7}$,
∵0<B<π,∴sinB=$\sqrt{1-co{s}^{2}B}$=$\frac{2\sqrt{6}}{7}$,
故选:C.
点评 本题考查利用正弦、余弦定理化简求值,向量的线性运算,以及重心的充要条件的应用,对数学思维的要求比较高,综合性强,难度大,易出错.

| 喜爱程度 | 非常喜欢 | 一般 | 不喜欢 |
| 人数 | 500 | 200 | 100 |
(1)求n的值;
(2)若不喜欢“如花姐”的1观众中抽取的5人中恰好3名男生(记为a1,a2,a3)2名女生(记为b1,b2),现将5人看成一个总体,从中随机选出2人,列出所有可能的结果;
(3)在(2)的条件下,求选出的2人中至少有1名女生的概率.
| A. | 28 | B. | -28 | C. | 56 | D. | -56 |
| A. | 等腰直角三角形 | B. | 等腰钝角三角形 | ||
| C. | 等边三角形 | D. | 不存在这样的三角形 |


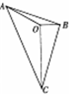 如图,已知O是△ABC内一点,∠AOB=150°,∠AOC=120°,向量$\overrightarrow{OA},\overrightarrow{OB}$,$\overrightarrow{OC}$的模分别为2,1,3,若$\overrightarrow{OC}$=m$\overrightarrow{OA}+n\overrightarrow{OB}$,则实数m+n的值为$-3-3\sqrt{3}$.
如图,已知O是△ABC内一点,∠AOB=150°,∠AOC=120°,向量$\overrightarrow{OA},\overrightarrow{OB}$,$\overrightarrow{OC}$的模分别为2,1,3,若$\overrightarrow{OC}$=m$\overrightarrow{OA}+n\overrightarrow{OB}$,则实数m+n的值为$-3-3\sqrt{3}$.