题目内容
6.已知数列{an}满足a3=-$\frac{1}{2}$,an+1=$\frac{1+{a}_{n}}{1-{a}_{n}}$(n∈N*),则a2的值为-3.分析 利用递推关系直接代入计算即可.
解答 解:∵a3=-$\frac{1}{2}$,an+1=$\frac{1+{a}_{n}}{1-{a}_{n}}$(n∈N*),
∴${a}_{3}=\frac{1+{a}_{2}}{1-{a}_{2}}$,即$-\frac{1}{2}$=$\frac{1+{a}_{2}}{1-{a}_{2}}$,
解得:a2=-3,
故答案为:-3.
点评 本题考查求数列的某项,利用递推关系式直接计算即可,属于基础题.

练习册系列答案
相关题目
17.二项式(x-$\frac{1}{x}$)8的展开式中x4的系数是( )
| A. | 28 | B. | -28 | C. | 56 | D. | -56 |
14.若△ABC中,a=2bcosC,且sin2B+sin2C=2sin2A,则该三角形一定为( )
| A. | 等腰直角三角形 | B. | 等腰钝角三角形 | ||
| C. | 等边三角形 | D. | 不存在这样的三角形 |
18.定义在R上的函数f(x)满足:f′(x)>1-f(x),f(0)=3,f′(x)是f(x)的导函数,则不等式exf(x)>ex+2(其中e为自然对数的底数)的解集为( )
| A. | {x|x>0} | B. | {x|x<0} | C. | {x|x<-1或x>1} | D. | {x|x<-1或0<x<1} |
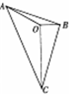 如图,已知O是△ABC内一点,∠AOB=150°,∠AOC=120°,向量$\overrightarrow{OA},\overrightarrow{OB}$,$\overrightarrow{OC}$的模分别为2,1,3,若$\overrightarrow{OC}$=m$\overrightarrow{OA}+n\overrightarrow{OB}$,则实数m+n的值为$-3-3\sqrt{3}$.
如图,已知O是△ABC内一点,∠AOB=150°,∠AOC=120°,向量$\overrightarrow{OA},\overrightarrow{OB}$,$\overrightarrow{OC}$的模分别为2,1,3,若$\overrightarrow{OC}$=m$\overrightarrow{OA}+n\overrightarrow{OB}$,则实数m+n的值为$-3-3\sqrt{3}$.