题目内容
经过点P(2,-3),作圆x2+y2=20的弦AB,且使得P平分AB,则弦AB所在直线的方程是___________.
2x-3y-13=0
把点P的坐标代入圆x2+y2=20的左边,得22+(-3)2=13<20,所以点P在圆O内.?
经过点P,被点P平分的圆的弦与OP垂直.
因为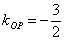 ,
,
所以弦AB所在直线的斜率是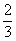 ,?
,?
弦AB所在的直线方程是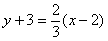 ,
,
即2x-3y-13=0.
经过点P,被点P平分的圆的弦与OP垂直.
因为
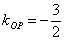 ,
,所以弦AB所在直线的斜率是
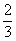 ,?
,?弦AB所在的直线方程是
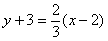 ,
,即2x-3y-13=0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
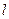 方程
方程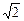 (x+y)+1+m=0与圆x2+y2=m的位置关系为
(x+y)+1+m=0与圆x2+y2=m的位置关系为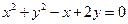 关于直线
关于直线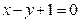 对称的圆的方程 .
对称的圆的方程 .