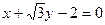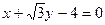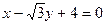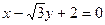题目内容
过圆(x-1)2+(y-1)2=1外一点P(2,3),向圆引两条切线切点为A、B. 求经过两切点的直线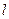 方程
方程
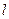 方程
方程设圆(-1)2+(y-1)2=1的圆心为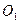 ,由题可知,以线段P
,由题可知,以线段P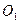 为直径的圆与与圆
为直径的圆与与圆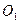 交于AB两点,线段AB为两圆公共弦,以P
交于AB两点,线段AB为两圆公共弦,以P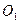 为直径的圆方程
为直径的圆方程
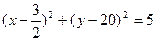 ①
①
已知圆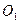 的方程为(x-1)2+(y-1)2="1 " ②
的方程为(x-1)2+(y-1)2="1 " ②
①②作差得x+2y-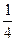 =0,即为所求直线
=0,即为所求直线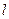 的方程。
的方程。
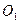 ,由题可知,以线段P
,由题可知,以线段P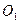 为直径的圆与与圆
为直径的圆与与圆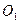 交于AB两点,线段AB为两圆公共弦,以P
交于AB两点,线段AB为两圆公共弦,以P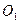 为直径的圆方程
为直径的圆方程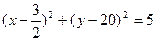 ①
① 已知圆
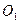 的方程为(x-1)2+(y-1)2="1 " ②
的方程为(x-1)2+(y-1)2="1 " ②①②作差得x+2y-
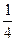 =0,即为所求直线
=0,即为所求直线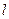 的方程。
的方程。同答案

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
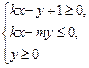 表示的平面区域的面积是
表示的平面区域的面积是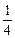
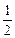
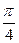

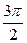
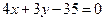 与圆心在原点的圆
与圆心在原点的圆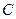 相切,求圆
相切,求圆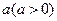 的两个定圆的切线长相等的点的轨迹是直线.
的两个定圆的切线长相等的点的轨迹是直线.

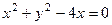 在点
在点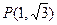 处的切线方程为( )
处的切线方程为( )