题目内容
【题目】如图，在长方体ABCD﹣A′B′C′D′中，AB=2，AD=1，AA′=1．证明直线BC′平行于平面D′AC，并求直线BC′到平面D′AC的距离．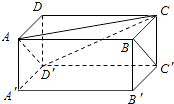 
【答案】解：解法一：因为ABCD﹣A′B′C′D′为长方体，故AB∥C′D′，AB=C′D′，
故ABC′D′为平行四边形，故BC′∥AD′，显然BC′不在平面D′AC内，
于是直线BC′平行于平面D′AC．
直线BC′到平面D′AC的距离即为点B到平面D′AC的距离，设为h，
考虑三棱锥D′﹣ABC的体积，以ABC为底面，可得三棱锥D′﹣ABC的体积为V= 
（ 
）= ，
而△AD′C中，AC=D′C= 
，AD′= 
，故△CAD′的底边AD′上的高为 
，
故△CAD′的面积S△CAD′= 
= 
，
所以，V= 
= h= 
，即直线BC′到平面D′AC的距离为 ．
解法二：以D′A′所在的直线为x轴，以D′C′所在的直线为y轴，以D′D所在的直线为z轴，
建立空间直角坐标系．
则由题意可得，点A（1，0，1 ）、B（1，2，1）、C（0，2，1）、C′（0，2，0）、D′（0，0，0）．
设平面D′AC的一个法向量为 
=（u，v，w），则由 ⊥ 
， ⊥ 
，可得 
， 
．
∵ =（1，0，1）， =（0，2，1），∴ 
，解得 
．
令v=1，可得 u=2，w=﹣2，可得 =（2，1，﹣2）．
由于 
=（﹣1，0，﹣1），∴ 
=﹣0，故有 ⊥ ．
再由BC′不在平面D′AC内，可得直线BC′平行于平面D′AC．
由于 
=（1，0，0），可得点B到平面D′AC的距离d= 
= 
= ，
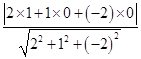故直线BC′到平面D′AC的距离为 ．
【解析】解法一：证明ABC′D′为平行四边形，可得BC′∥AD′，再利用直线和平面平行的判定定理证得直线BC′平行于平面D′AC． 所求的距离即点B到平面D′AC的距离，设为h，再利用等体积法求得h的值．
解法二：建立空间直角坐标系，求出平面D′AC的一个法向量为 
=（2，1，﹣2），再根据 
=﹣0，可得 ⊥ 
，可得直线BC′平行于平面D′AC．求出点B到平面D′AC的距离d= 
的值，即为直线BC′到平面D′AC的距离．
【考点精析】关于本题考查的直线与平面平行的判定，需要了解平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行才能得出正确答案．
