Question

【题目】已知椭圆C的两个焦点分别为F1（﹣1，0）、F2（1，0），短轴的两个端点分别为B1 ， B2
（1）若△F1B1B2为等边三角形，求椭圆C的方程；
（2）若椭圆C的短轴长为2，过点F2的直线l与椭圆C相交于P，Q两点，且 ，求直线l的方程．

Answer 1

【答案】
（1）解：设椭圆C的方程为 ．

根据题意知 ，解得 ，

故椭圆C的方程为 ．

（2）解：由2b=2，得b=1，所以a2=b2+c2=2，得椭圆C的方程为 ．

当直线l的斜率不存在时，其方程为x=1，不符合题意；

当直线l的斜率存在时，设直线l的方程为y=k（x﹣1）．

由 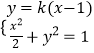，得（2k2+1）x2﹣4k2x+2（k2﹣1）=0．

设P（x1，y1），Q（x2，y2），则

，

因为 ，所以 ，即

=

=

= ，解得 ，即k= ．

故直线l的方程为 或 ．

【解析】（1）由△F1B1B2为等边三角形可得a=2b，又c=1，集合a2=b2+c2可求a2 ， b2 ， 则椭圆C的方程可求；（2）由给出的椭圆C的短轴长为2，结合c=1求出椭圆方程，分过点F2的直线l的斜率存在和不存在讨论，当斜率存在时，把直线方程和椭圆方程联立，由根与系数关系写出两个交点的横坐标的和，把 转化为数量积等于0，代入坐标后可求直线的斜率，则直线l的方程可求．
【考点精析】本题主要考查了一般式方程和椭圆的标准方程的相关知识点，需要掌握直线的一般式方程：关于的二元一次方程（A，B不同时为0）；椭圆标准方程焦点在x轴：，焦点在y轴：才能正确解答此题．