题目内容
（本小题满分12分）
在△ABC中，角A、B、C所对边分别为a，b，c，已知
，
（1）求角C的大小；
（2）若最长边的边长为l0 ，求△ABC的面积.
在△ABC中，角A、B、C所对边分别为a，b，c，已知
，（1）求角C的大小；
（2）若最长边的边长为l0 ，求△ABC的面积.
（1）
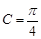；（2）△ABC的面积
=
。
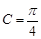；（2）△ABC的面积=。本试题主要是考查了解三角形的运用。
（1）由于由 得
，结合两角和差的关系式，和内角和定理得到结论。
（2）∵A为钝角，最长边长为a =10 由
，得到b的值，然后结合面积公式得到结论。
解：（1）由 得
cosC＝cos[π－（A＋B）]＝－cos（A＋B）
= －（
）
= －(
)=
∵
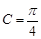， ∴ ……………………6分
（2）∵A为钝角，最长边长为a =10 ……………………7分
由 ，∴
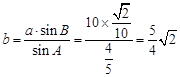， ……………………9分
△ABC的面积=……………12分
（1）由于由
得，结合两角和差的关系式，和内角和定理得到结论。（2）∵A为钝角，最长边长为a =10 由
，得到b的值，然后结合面积公式得到结论。解：（1）由
得cosC＝cos[π－（A＋B）]＝－cos（A＋B）
= －（
）= －(
)=∵
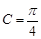， ∴ ……………………6分（2）∵A为钝角，最长边长为a =10 ……………………7分
由
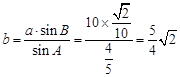，∴， ……………………9分△ABC的面积
=……………12分
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
的面积
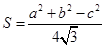，则
= 
分别为内角A.B.C所对的边，且满足
②
③
试从中选出两个可以确定△ABC的条件写出你的选择，并以此为依据求△ABC的面积（只需写出一个选定方案即可，选多种方案以第一种方案记分）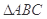
为钝角三角形，三边长分别为2，3，
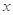，则
的值；
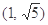
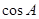的值.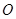
的半径是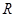
， 它的内接三角形
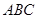中， 有
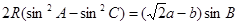成立，求角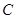
的大小及三角形面积
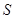的最大值. 
，
的最大值和最小正周期；
为
的三个内角，若
，且
为锐角，求
的值。