题目内容
(本小题满分13分)如图,在三棱柱ABC—A1B1C1中,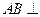 侧面BB1C1C,已知AB=BC=1,BB1=2,
侧面BB1C1C,已知AB=BC=1,BB1=2,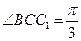 ,E为CC1的中点。
,E为CC1的中点。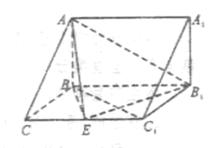
(1)求证: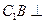 平面ABC;
平面ABC;
(2)求二面角A—B1E—B的大小。
解:(1)因为AB⊥侧面 ,
, 侧面
侧面 ,故AB⊥BCl,
,故AB⊥BCl,
在△BCCl中,BC=1, ,
, ,
,
可得△BCE为等边三角形,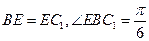 ,所以BC⊥BCl.
,所以BC⊥BCl.
而BC AB=B,∴C1B⊥平面AB C.…………………………6分
AB=B,∴C1B⊥平面AB C.…………………………6分
(2)在△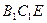 中,
中,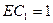 ,
,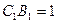 ,
,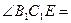
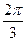 ,
,
∴
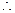 BE⊥EBl.
BE⊥EBl.
又∵AB⊥侧面BBlC1C,∴AB⊥BlE,
又AB BE=B,∴B1E⊥平面ABE,∴AE⊥BlE,
BE=B,∴B1E⊥平面ABE,∴AE⊥BlE,
∴∠AEB即是二面角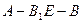 的平面角.
的平面角.
在Rt△ABE中,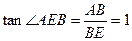 ,故
,故 .
.
所以二面角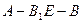 的大小为
的大小为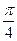 .……………12分(亦可建立空间直角坐标系求解)
.……………12分(亦可建立空间直角坐标系求解)
解析

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
如图所示,在正方体ABCD-A1B1C1D1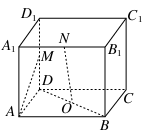
中,O是底面正方形ABCD的中心,M是D1D的中点,N是A1B1上的动点,则直线NO、AM的位置关系是( )
| A.平行 | B.相交 |
| C.异面垂直 | D.异面不垂直 |
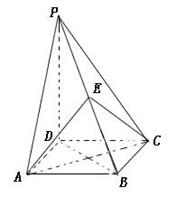
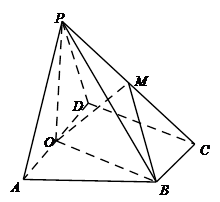
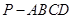 的底面是正方形,
的底面是正方形,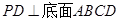 ,点E在棱PB上.若AB=
,点E在棱PB上.若AB=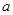 ,
,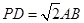
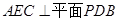 ;
; 
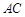 是圆
是圆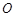 的直径,点
的直径,点 在圆
在圆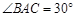 ,
,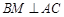 交
交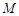 ,
,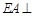 平面
平面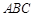 ,
,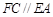 ,
,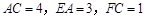 .
.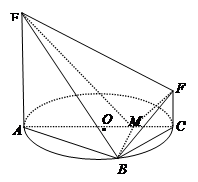
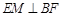 ;
;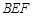 与平面
与平面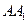 、
、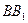 为圆柱
为圆柱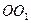 的母线,
的母线, 是底面圆
是底面圆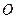 的直径,
的直径,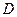 、
、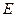 分别是
分别是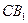 的中点,
的中点,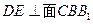 .
.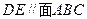 ;
;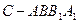 与圆柱
与圆柱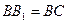 ,求
,求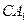 与面
与面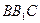 所成角的正弦值.
所成角的正弦值.
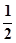 AD=1,CD=
AD=1,CD=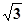 .
.
 中,
中,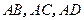 两两垂直,平面
两两垂直,平面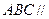 平面
平面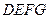 ,
,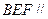 平面
平面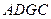 ,
, .
.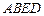 是正方形;
是正方形; 是否四点共面,并说明为什么?
是否四点共面,并说明为什么?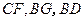 ,求证:
,求证: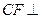 平面
平面 .
.
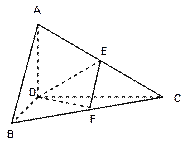
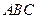 的边长为4,
的边长为4,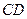 是
是 边上的高,
边上的高,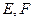 分别是
分别是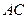 和
和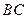 边的中点,现将△
边的中点,现将△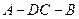 .
.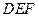 的位置关系,并说明理由;
的位置关系,并说明理由;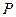 ,使
,使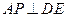 ?证明你的结论.
?证明你的结论.
 B1D^平面PQR;
B1D^平面PQR;