题目内容
如图,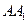 、
、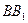 为圆柱
为圆柱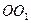 的母线,
的母线, 是底面圆
是底面圆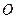 的直径,
的直径,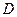 、
、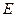 分别是
分别是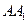 、
、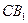 的中点,
的中点,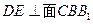 .
.
(1)证明: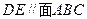 ;
;
(2)求四棱锥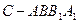 与圆柱
与圆柱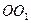 的体积比;
的体积比;
(3)若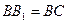 ,求
,求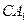 与面
与面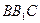 所成角的正弦值.
所成角的正弦值.
解:(1)证明:连结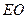 ,
,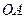 .
.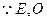 分别为
分别为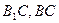 的中点,∴
的中点,∴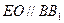 .
.
又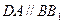 ,且
,且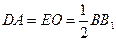 .∴四边形
.∴四边形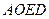 是平行四边形,
是平行四边形,
即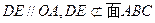 . ∴
. ∴ . ………………………4分
. ………………………4分
(2)由题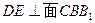 ,且由(1)知
,且由(1)知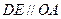 .∴
.∴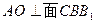 ,∴
,∴ 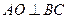 ,∴
,∴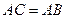 .
.
因 是底面圆
是底面圆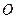 的直径,得
的直径,得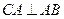 ,且
,且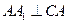 ,
,
∴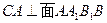 ,即
,即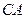 为四棱锥的高.设圆柱高为
为四棱锥的高.设圆柱高为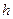 ,底半径为
,底半径为 ,
,
则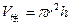 ,
,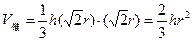
∴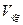 :
: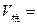
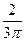 . ………………………9分
. ………………………9分
(3)解一:由(1)(2)可知,可分别以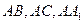 为坐标轴建立空间直角标系,如图
为坐标轴建立空间直角标系,如图
设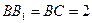 ,则
,则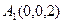 ,
,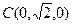 ,
,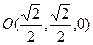 ,从而
,从而 ,
,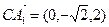 ,由题,
,由题,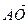 是面
是面 的法向量,设所求的角为
的法向量,设所求的角为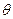 .
.
则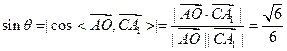 . …………………14分
. …………………14分
解二:作过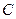 的母线
的母线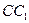 ,连结
,连结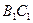 ,则
,则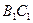 是上底面圆
是上底面圆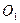 的直径,连结
的直径,连结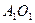 ,
,
得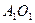
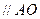 ,又
,又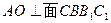 ,∴
,∴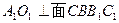 ,连结
,连结 ,
,
则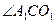 为
为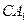 与面
与面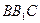 所成的角,设
所成的角,设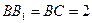 ,则
,则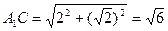 ,
,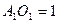 .……12分
.……12分
在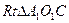 中,
中,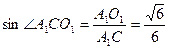

解析

练习册系列答案
相关题目
已知向量a=(1,1,0),b=(-1,0,2),且ka+b与2a-b互相垂直,则k值是( )
| A.1 | B.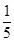 | C.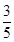 | D.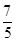 |
 ∩平面
∩平面 =AB,PQ⊥
=AB,PQ⊥
 中,
中, ⊥面
⊥面 ,
, ,
, 上的点,且
上的点,且 ⊥面
⊥面 ,
, 、
、 交于点
交于点 .
. ⊥
⊥ ;
;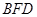 .
.
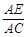 =
= =λ (0<λ<1).
=λ (0<λ<1).
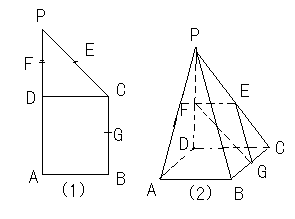

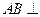 侧面BB1C1C,已知AB=BC=1,BB1=2,
侧面BB1C1C,已知AB=BC=1,BB1=2,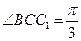 ,E为CC1的中点。
,E为CC1的中点。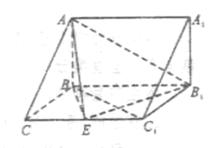
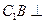 平面ABC;
平面ABC; B。
B。