题目内容
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点.
(1)求证: B1D^平面PQR;
B1D^平面PQR;
(2)设二面角B1-PR-Q的大小为q,求|cosq|.
解:(1)在正方体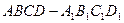 中,以点A为原点,分别以
中,以点A为原点,分别以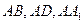 所
所
在直线为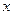 轴,
轴,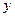 轴,
轴, 轴,建立如图所示的空间直角坐标系。
轴,建立如图所示的空间直角坐标系。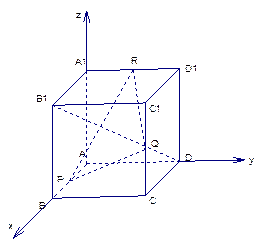
由于棱长为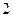 ,所以
,所以 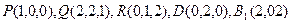
所以,
因为 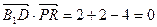
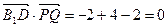
所以 
即: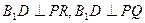
又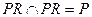 且
且 ,所以,
,所以,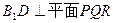
(2)由(1)知,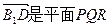 的一个法向量
的一个法向量
设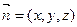 是平面
是平面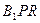 的一个法向量,因为
的一个法向量,因为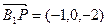
则由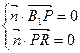 得
得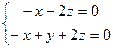
取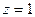 则
则 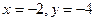
即:平面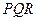 的一个法向量
的一个法向量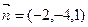
所以 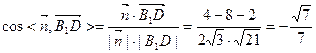
所以 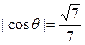
解析

练习册系列答案
相关题目
已知向量a=(1,1,0),b=(-1,0,2),且ka+b与2a-b互相垂直,则k值是( )
| A.1 | B.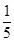 | C.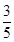 | D.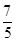 |
在z轴上与点A(-4,1,7)和点B(3,5,-2)等距离的点C的坐标为( )
| A.(0,0,1) |
| B.(0,0,2) |
C.(0,0,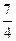 ) ) |
D.(0,0,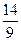 ) ) |
 中,
中, ⊥面
⊥面 ,
, ,
, 上的点,且
上的点,且 ⊥面
⊥面 ,
, 、
、 交于点
交于点 .
. ⊥
⊥ ;
; .
.
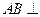 侧面BB1C1C,已知AB=BC=1,BB1=2,
侧面BB1C1C,已知AB=BC=1,BB1=2,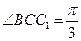 ,E为CC1的中点。
,E为CC1的中点。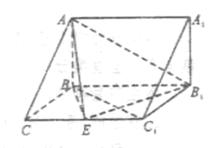
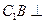 平面ABC;
平面ABC; B。
B。
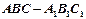 的三视图如图所示,
的三视图如图所示, 其中正视图
其中正视图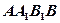 和侧视图
和侧视图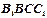 均为矩形,俯视图
均为矩形,俯视图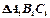 中,
中,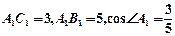 。
。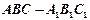 中,求证:
中,求证: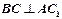 ;
;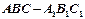 中,若
中,若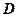 是底边
是底边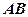 的中点,求证:
的中点,求证: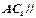 平面
平面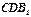 ;
;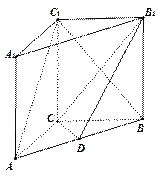
 本小题满分12分)如图,在三棱柱
本小题满分12分)如图,在三棱柱 中,
中, 面
面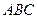 ,
,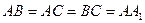 ,
,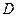 ,
,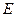 分别为
分别为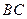 ,
,
 的中点.
的中点.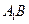 ∥平面
∥平面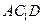 ; (2)求证:
; (2)求证: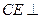 平面
平面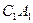 与平面
与平面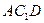 所成的角的
所成的角的 正弦值.
正弦值.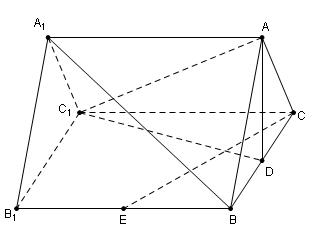
 FE交AP于E,交DP于F.求证:四边形BCFE是梯形.
FE交AP于E,交DP于F.求证:四边形BCFE是梯形.