题目内容
将一个长宽分别是a，b(0＜b＜a)的铁皮的四角切去相同的正方形，然后折成一个无盖的长方体的盒子，若这个长方体的外接球的体积存在最小值，则
的取值范围是________．
的取值范围是________．
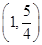
设切去正方形的边长为x，x∈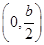
，
则该长方体外接球的半径为
r2＝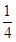
[(a－2x)2＋(b－2x)2＋x2]
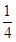＝ [9x2－4(a＋b)x＋a2＋b2]，在x∈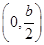
存在最小值时，必有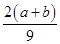
＜
，
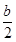解得＜
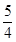，又0＜b＜a⇒＞1，
故的取值范围是.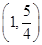
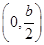，则该长方体外接球的半径为
r2＝
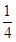[(a－2x)2＋(b－2x)2＋x2]＝
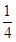[9x2－4(a＋b)x＋a2＋b2]，在x∈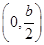存在最小值时，必有
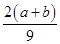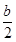＜，解得
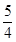＜，又0＜b＜a⇒＞1，故
的取值范围是.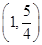
练习册系列答案
相关题目
<-1.
内单调递减，求a的取值范围；
＝C，则称函数f(x)在D上的几何平均数为C.已知f(x)＝x3，x∈[1,2]，则函数f(x)＝x3在[1,2]上的几何平均数为( )
函数f(x) =max{|x+1|，|x-2|}(x∈R)的最小值是（ ）
，若a，b，c互不相等，且
，则
的取值范围为（ ）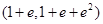
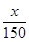＋2是否符合公司要求的奖励函数模型，并说明原因；
作为奖励函数模型，试确定最小的正整数a的值．
定义在
上，其导函数为
，且
，当
时，
,则关于
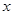的不等式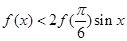
的解集为 ．