题目内容
8.已知$\left\{\begin{array}{l}{sinα+sinβ=\frac{1}{2}}\\{y=co{s}^{2}α-sinβ}\end{array}\right.$,求值域.分析 利用已知条件,化简所求表达式只有一个角的三角函数的形式,通过三角函数以及二次函数的性质求解表达式的最值即可.
解答 解:sinα+sinβ=$\frac{1}{2}$,则$y=co{s}^{2}α+sinα-\frac{1}{2}$=-sin2α+sinα+$\frac{1}{2}$=-(sinα-$\frac{1}{2}$)2+$\frac{3}{4}$.
∵sinα+sinβ=$\frac{1}{2}$,∴sinα∈[-$\frac{1}{2}$,1],
∴sinα=$\frac{1}{2}$时,函数取得最大值:$\frac{3}{4}$.
sinα=-1时,函数取得最小值:-$\frac{3}{2}$.
函数的值域为[-$\frac{3}{2}$,$\frac{3}{4}$].
点评 本题考查三角函数的最值的求法,涉及二次函数的性质的应用,考查计算能力.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
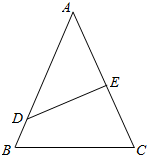 某校把一块形状为正三角形的边角地ABC开辟为生态园,如图所示,其中AB=2a,DE把三角形分成面积相等的两个部分,D在线段AB上,E在线段AC上.
某校把一块形状为正三角形的边角地ABC开辟为生态园,如图所示,其中AB=2a,DE把三角形分成面积相等的两个部分,D在线段AB上,E在线段AC上.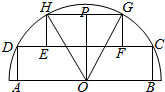 如图,一块半径为2米的半圆形钢板,O为圆心,现从中截出两块内接矩形部件ABCD和EFGH,且HG=2FG,点P为GH的中点,∠POG=θ.
如图,一块半径为2米的半圆形钢板,O为圆心,现从中截出两块内接矩形部件ABCD和EFGH,且HG=2FG,点P为GH的中点,∠POG=θ.