题目内容
18.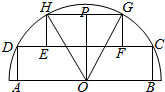 如图,一块半径为2米的半圆形钢板,O为圆心,现从中截出两块内接矩形部件ABCD和EFGH,且HG=2FG,点P为GH的中点,∠POG=θ.
如图,一块半径为2米的半圆形钢板,O为圆心,现从中截出两块内接矩形部件ABCD和EFGH,且HG=2FG,点P为GH的中点,∠POG=θ.(1)当θ=15°时,求矩形ABCD的面积;
(2)设△OGH的面积为S,当θ变化时,求y=S+BC的最大值.
分析 (1)、当θ=15°时,GF=PG=2sin15°,OP=2cos15°,从而求得BC=2cos15°-2sin15°=2$\sqrt{1-sin30°}$=$\sqrt{2}$;再求矩形ABCD的面积;
(2)可知S=$\frac{1}{2}$×HG×OP=4sinθcosθ,BC=2cosθ-2sinθ,从而可得y=S+BC=4sinθcosθ+2cosθ-2sinθ,再利用换元法令cosθ-sinθ=t(0<t<1),则2sinθcosθ=1-t2,从而化为二次函数的最值问题.
解答 解:(1)、当θ=15°时,
GF=PG=2sin15°,OP=2cos15°,
BC=2cos15°-2sin15°
=2$\sqrt{1-sin30°}$
=$\sqrt{2}$;
故OB=$\sqrt{{2}^{2}-2}$=$\sqrt{2}$,
故矩形ABCD的面积S=2$\sqrt{2}$×$\sqrt{2}$=4.
(2)、由题意,
S=$\frac{1}{2}$×HG×OP
=$\frac{1}{2}$×2×2sinθ×2cosθ
=4sinθcosθ,
BC=2cosθ-2sinθ,
故y=S+BC=4sinθcosθ+2cosθ-2sinθ
令cosθ-sinθ=t(0<t<1),则2sinθcosθ=1-t2,
则y=2(1-t2)+2t
=2(-t2+t+1)=-2(t-$\frac{1}{2}$)2+$\frac{3}{2}$;
故当t=$\frac{1}{2}$时,y=S+BC取得最大值$\frac{3}{2}$.
点评 本题考查了三角函数的化简与应用,同时考查了二次函数的最值求法及换元法的应用,属于中档题.

练习册系列答案
相关题目
3.在△ABC中,若sinC=$\frac{3}{5}$,c=3,则△ABC外接圆的半径为( )
| A. | 5 | B. | $\frac{5}{2}$ | C. | $\frac{25}{4}$ | D. | 25 |