Question

【题目】已知数列{an}中，a1=1，an+1= ．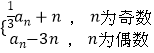
（1）证明：数列{a2n﹣ }是等比数列；
（2）求a2n及a2n﹣1 ．

Answer 1

【答案】
（1）证明：设 ，则 ，

因为 ，

所以数列 是以 为首项， 为公比的等比数列．

（2）解：由（1）的 ，即 ．

由 得 ．

【解析】1、根据已知条件结合等比数列的定义验证是一个常数，即可得证。
2、利用（1）的结论可求出结果。
【考点精析】解答此题的关键在于理解等比关系的确定的相关知识，掌握等比数列可以通过定义法、中项法、通项公式法、前n项和法进行判断，以及对数列的通项公式的理解，了解如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．