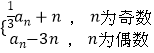题目内容
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD的平行四边形,∠ADC=60°, ![]() ,PA⊥面ABCD,E为PD的中点.
,PA⊥面ABCD,E为PD的中点.
(Ⅰ)求证:AB⊥PC
(Ⅱ)若PA=AB= ![]() ,求三棱锥P﹣AEC的体积.
,求三棱锥P﹣AEC的体积.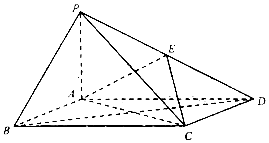
【答案】(Ⅰ)证明:因为PA⊥面ABCD,又AB平面ABCD,
所以AB⊥PA,
又因为∠ABC=∠ADC=60°, ![]() ,
,
在△ABC中,由余弦定理有:
AC2=AB2+BC2﹣2ABBCcos60°=BC2﹣AB2
所以AB2+AC2=BC2,
即:AB⊥AC,
又因为PA∩AC=A,又PA平面PAC,AC平面PAC,
所以AB⊥平面PAC,
又PC平面PAC,所以AB⊥PC.
(Ⅱ)解:由已知有: ![]() ,
,
所以PA=AB=2,AD=4,因为PA⊥面ABCD
且E为PD的中点,所以E点到平面ADC的距离为 ![]() ,
,
所以三棱锥P﹣AEC的体积:
VP﹣AEC=VD﹣AEC=VE﹣ADC= ![]()
= ![]() ×
× ![]() .
.
【解析】(1)因为PA⊥面ABCD,则AB⊥PA,根据边角的大小关系,由余弦定理可证出△ABC为直角三角形,即AB⊥AC,从而可证出AB⊥面PAC,即AB⊥PC,(2)由已知可得出其各边的大小,由于E为PD的中点,则不难得出E到面ADC的距离为1,VP﹣AEC=VD﹣AEC=VE﹣ADC= ![]() S △ A D C,即可得出结果.
S △ A D C,即可得出结果.
【考点精析】本题主要考查了空间中直线与直线之间的位置关系的相关知识点,需要掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点才能正确解答此题.

练习册系列答案
相关题目