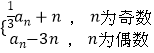题目内容
【题目】已知椭圆 ![]() 的左右顶点分别为A,B,点P为椭圆上异于A,B的任意一点.
的左右顶点分别为A,B,点P为椭圆上异于A,B的任意一点.
(Ⅰ)求直线PA与PB的斜率之积;
(Ⅱ)过点 ![]() 作与x轴不重合的任意直线交椭圆E于M,N两点.证明:以MN为直径的圆恒过点A.
作与x轴不重合的任意直线交椭圆E于M,N两点.证明:以MN为直径的圆恒过点A.
【答案】解:(Ⅰ) ![]() .设点P(x,y)(y≠0),则有
.设点P(x,y)(y≠0),则有 ![]() ,即
,即 ![]() ,
,
∴ ![]() =
= ![]()
(Ⅱ)证明:设M(x1,y1),N(x2,y2),
∵MN与x轴不重合,
∴设直线 ![]() ,
,
由 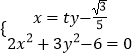 化简得,
化简得,
![]() ;
;
由题意可知△>0成立,且 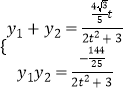 ;
;
![]()
= ![]() ;
;
将 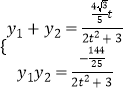 代入上式并化简得,
代入上式并化简得,
![]() .
.
∴AM⊥AN,即以MN为直径的圆恒过点A
【解析】(Ⅰ)根据已知条件得到两个直线的斜率再将两个式子的乘积转化为已知的形式进而求得结果。(Ⅱ)由已知通过向量数量积为零证明两条直线垂直从而得到以MN为直径的圆恒过直线外的一点A。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目