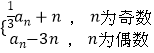题目内容
【题目】设曲线y=xn+1(n∈N*)在点(1,1)处的切线与x轴的交点的横坐标为xn , 令an=lgxn , 则a1+a2+…+a99的值为 .
【答案】-2
【解析】解:∵曲线y=xn+1(n∈N*), ∴y′=(n+1)xn , ∴f′(1)=n+1,
∴曲线y=xn+1(n∈N*)在(1,1)处的切线方程为y﹣1=(n+1)(x﹣1),
该切线与x轴的交点的横坐标为xn= ![]() ,
,
∵an=lgxn ,
∴an=lgn﹣lg(n+1),
∴a1+a2+…+a99
=(lg1﹣lg2)+(lg2﹣lg3)+(lg3﹣lg4)+(lg4﹣lg5)+(lg5﹣lg6)+…+(lg99﹣lg100)
=lg1﹣lg100=﹣2.
所以答案是:﹣2.
【考点精析】关于本题考查的数列的前n项和,需要了解数列{an}的前n项和sn与通项an的关系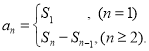 才能得出正确答案.
才能得出正确答案.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目