题目内容
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
![]() 求椭圆
求椭圆![]() 的方程;
的方程;
![]() 已知
已知![]() 与
与![]() 为平面内的两个定点,过点
为平面内的两个定点,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() (2)6
(2)6
【解析】试题分析:(1)由椭圆定义得到动圆圆心![]() 的轨迹
的轨迹![]() 的方程;(2)设
的方程;(2)设![]() 的方程为
的方程为![]() ,联立可得
,联立可得![]() ,通过根与系数的关系表示弦长进而得到四边形
,通过根与系数的关系表示弦长进而得到四边形![]() 面积的表达式,利用换元法及均值不等式求最值即可.
面积的表达式,利用换元法及均值不等式求最值即可.
试题解析:
解:![]() 由
由![]() 可得,
可得,![]() ,又因为
,又因为![]() ,所以
,所以![]() .
.
所以椭圆![]() 方程为
方程为![]() ,又因为
,又因为![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() .
.
所以![]() ,所以
,所以![]() ,故椭圆方程为
,故椭圆方程为![]() .
.
![]() 方法一:设
方法一:设![]() 的方程为
的方程为![]() ,联立
,联立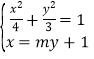 ,
,
消去![]() 得
得![]() ,设点
,设点![]() ,
,
有![]()
![]() ,
,
所以![]() 令
令![]() ,
,
有![]() ,由
,由
函数![]() ,
,![]()
![]()
故函数![]() ,在
,在![]() 上单调递增,
上单调递增,
故![]() ,故
,故![]()
当且仅当![]() 即
即![]() 时等号成立,
时等号成立,
四边形![]() 面积的最大值为
面积的最大值为![]() .
.
方法二:设![]() 的方程为
的方程为![]() ,联立
,联立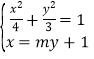 ,
,
消去![]() 得
得![]() ,设点
,设点![]() ,
,
有![]()
有![]() ,
,
点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
从而四边形![]() 的面积
的面积
![]()
令![]() ,
,
有![]() ,
,
函数![]() ,
,![]()
![]()
故函数![]() ,在
,在![]() 上单调递增,
上单调递增,
有![]() ,故
,故![]() 当且仅当
当且仅当![]() 即
即![]() 时等号成立,四边形
时等号成立,四边形![]() 面积的最大值为
面积的最大值为![]() .
.
方法三:①当![]() 的斜率不存在时,
的斜率不存在时,![]()
此时,四边形![]() 的面积为
的面积为![]() .
.
②当![]() 的斜率存在时,设
的斜率存在时,设![]() 为:
为:![]() ,
,![]()
则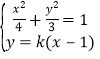
![]()
![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 的面积
的面积
![]() ,
,
令 ![]() 则
则 ![]()
![]() ,
,![]()
![]() ,
,
![]() ,
,
综上,四边形![]() 面积的最大值为
面积的最大值为![]() .
.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
【题目】某音乐院校举行“校园之星”评选活动,评委由本校全体学生组成,对![]() 两位选手,随机调查了20个学生的评分,得到下面的茎叶图:
两位选手,随机调查了20个学生的评分,得到下面的茎叶图:

所得分数 | 低于60分 | 60分到79分 | 不低于80分 |
分流方向 | 淘汰出局 | 复赛待选 | 直接晋级 |
(1)通过茎叶图比较![]() 两位选手所得分数的平均值及分散程度(不要求计算出具体值,得出结论即可);
两位选手所得分数的平均值及分散程度(不要求计算出具体值,得出结论即可);
(2)举办方将会根据评分结果对选手进行三向分流,根据所得分数,估计![]() 两位选手中哪位选手直接晋级的概率更大,并说明理由.
两位选手中哪位选手直接晋级的概率更大,并说明理由.