题目内容
【题目】2020年是中国传统的农历“鼠年”,有人用3个圆构成“卡通鼠”的形象,如图:![]() 是圆Q的圆心,圆Q过坐标原点O;点L、S均在x轴上,圆L与圆S的半径都等于2,圆S、圆L均与圆Q外切.已知直线l过点O.
是圆Q的圆心,圆Q过坐标原点O;点L、S均在x轴上,圆L与圆S的半径都等于2,圆S、圆L均与圆Q外切.已知直线l过点O.

(1)若直线l与圆L、圆S均相切,则l截圆Q所得弦长为__________;
(2)若直线l截圆L、圆S、圆Q所得弦长均等于d,则![]() __________.
__________.
【答案】3 ![]()
【解析】
圆![]() 与圆
与圆![]() 关于原点对称,直线
关于原点对称,直线![]() 过原点,只要与一个圆相切,必与另一圆相切.求出圆
过原点,只要与一个圆相切,必与另一圆相切.求出圆![]() 与圆
与圆![]() 的圆心坐标,
的圆心坐标,
(1)求出切线方程后,求出![]() 到切线
到切线![]() 的距离后由勾股定理得弦长.
的距离后由勾股定理得弦长.
(2)设出直线![]() 方程,由三个弦长相等得直线方程,从而可得弦长
方程,由三个弦长相等得直线方程,从而可得弦长![]() .
.
由题意圆![]() 与圆
与圆![]() 关于原点对称,设
关于原点对称,设![]() ,则
,则![]() ,
,![]() ,
,
即![]() ,∴
,∴![]() .
.
(1)设![]() 方程为
方程为![]() ,即
,即![]() ,由
,由![]() 得
得![]() ,由对称性不妨取
,由对称性不妨取![]() ,
,![]() 方程为
方程为![]() ,
,![]() ,圆心
,圆心![]() 到
到![]() 的距离为
的距离为 ,∴弦长为
,∴弦长为![]() ;
;
(2)同(1)设直线![]() 方程为
方程为![]() ,点
,点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,直线截圆
,直线截圆![]() 得弦长为
得弦长为![]() ,点
,点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,直线截圆
,直线截圆![]() 得弦长为
得弦长为![]() ,由题意
,由题意 ,解得
,解得![]() ,∴
,∴ .
.
故答案为:3;![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某地区某农产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
年产量y(万吨) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(Ⅰ)根据表中数据,建立![]() 关于的线性回归方程
关于的线性回归方程![]() ;
;
(Ⅱ)根据线性回归方程预测2019年该地区该农产品的年产量.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: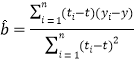 ,
,![]() .(参考数据:
.(参考数据:![]() ,计算结果保留小数点后两位)
,计算结果保留小数点后两位)
