题目内容
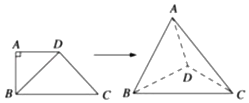
【题目】如图,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A﹣BCD,则在三棱锥A﹣BCD中,下列判断正确的是_____.(写出所有正确的序号)

①平面ABD⊥平面ABC
②直线BC与平面ABD所成角是45°
③平面ACD⊥平面ABC
④二面角C﹣AB﹣D余弦值为![]()
【答案】②③④
【解析】
①反证法,假设平面![]() 平面
平面![]() ,容易推出
,容易推出![]() 垂直于平面
垂直于平面![]() ,从而
,从而![]() ,出矛盾;
,出矛盾;
②利用几何法找到其平面角为![]() ,求解即可判断;
,求解即可判断;
③证明![]() 平面
平面![]() ,从而得到平面
,从而得到平面![]() 平面
平面![]() ;
;
④证明![]() 为二面角
为二面角![]() 的平面角,求解三角形得二面角的余弦值判断.
的平面角,求解三角形得二面角的余弦值判断.
在四边形ABCD中,由已知可得∠DBC=45°,假设平面ABD⊥平面ABC,
又平面ABD⊥平面BCD,且平面ABD∩平面BDC=BC,可得BC⊥平面ABD,
有∠DBC=90°,与∠DBC=45°矛盾,则假设错误,故①错误;
在四边形ABCD中,由已知可得BD⊥DC,
又平面ABD⊥平面BCD,且平面ABD∩平面BCD=BD,则DC⊥平面ABD,
∠DBC为直线BC与平面ABD所成角是45°,故②正确;
由判断②时可知,DC⊥平面ABD,则DC⊥AB,又BA⊥AD,AD∩DC=D,则AB⊥平面ADC,
而AB平面ABC,则平面ACD⊥平面ABC,故③正确;
由判断③时可知,AB⊥平面ADC,则∠DAC为二面角C﹣AB﹣D的平面角,
设AD=AB=1,则BD=DC![]() ,由DC⊥AD,得AC
,由DC⊥AD,得AC![]() ,得cos∠DAC
,得cos∠DAC![]() ,故④正确.
,故④正确.
∴判断正确的是②③④.
故答案为:②③④.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目

