题目内容

19．函数f（x）=x2+lnx的零点个数为（　　）
A．0B．1C．2D．3

分析 作函数y=x2与y=-lnx的图象，从而利用数形结合求解．

解答 解：作函数y=x2与y=-lnx的图象如下，
结合图象可知，函数的图象只有一个交点，
故函数f（x）=x2+lnx的零点个数为1，
故选B．

点评 本题考查了函数的零点的判断与应用，应用了数形结合的思想应用．

练习册系列答案
相关题目
9．设全集U={1，2，3，4，5，6}，A={2，4，5}，B={1，2，5}，则A∩B={2，5}，A∪（∁UB）={2，3，4，5，6}．
10．已知函数f（x）=ax2+b|x-1|，其中a，b∈（-4，4）且a≠0
（Ⅰ）当a∈（0，4），b=1时，求函数f（x）在[0，2]上的最小值；
（Ⅱ）若存在实数c，使函数g（x）=f（x）-c有四个不同的零点，求a+b的取值范围．
7．已知函数f（x）=$\frac{{{x^2}+3}}{x+1}$．
（1）求函数f（x）在区间[0，2]上的最值；
（2）若关于x的方程（x+1）f（x）-ax=0在区间（1，4）内有两个不等实根，求实数a的取值范围．
14．对于函数y=g（x），部分x与y的对应关系如下表：
x123456
y247518
数列{xn}满足：x1=2，且对于任意n∈N*，点（xn，xn+1）都在函数y=g（x）的图象上，则x1+x2+…+x2015=（　　）
A．4054B．5046C．5075D．6047
4．已知定义在R上的函数$f（x）={（\frac{1}{2}）^{|x-m|}}-1$（m为实数）为偶函数，记a=f（log0.53），b=f（log25），c=f（2m），则a，b，c的大小关系为（　　）
A．a＜b＜cB．b＜a＜cC．c＜a＜bD．a＜c＜b
11．已知$f（x）=sin（\frac{π}{6}-2x）+1-2{cos^2}x$．
（Ⅰ）求函数f（x）的单调递减区间；
（Ⅱ）在△ABC中，a，b，c分别是角A，B，C的对边，且$a=1，b+c=2，f（A）=-\frac{1}{2}$，求△ABC的面积．
8．计算：
（1）log427×log58×log325
（2）（${a^{\frac{2}{3}}}{b^{\frac{1}{2}}}$）•（-3${a^{\frac{1}{2}}}{b^{\frac{1}{3}}}$）÷（$\frac{1}{3}{a^{\frac{1}{6}}}{b^{\frac{5}{6}}}$）
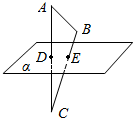9．如图所示，D、E分别是△ABC的边AC、BC上的点，平面α经过D、E两点．
（1）求作直线AB与平面α的交点P；
（2）求证：D、E、P三点共线．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网