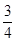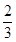题目内容
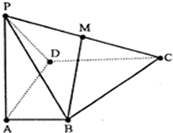
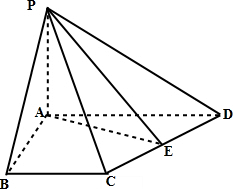
如图所示,四棱锥P-ABCD中,AB⊥AD,CD⊥AD,PA⊥底面ABCD,PA=AD=CD=2AB=2,M为PC的中点.
(1)求证:BM∥平面PAD;
(2)在侧面PAD内找一点N,使MN⊥平面PBD;
(3)求直线PC与平面PBD所成角的正弦.
(1)求证:BM∥平面PAD;
(2)在侧面PAD内找一点N,使MN⊥平面PBD;
(3)求直线PC与平面PBD所成角的正弦.

(1)证明:取PD的中点E,连接EM,EA,则EM∥AB,且EM=AB
所以四边形ABME为平行四边形,所以BM∥AE
又AE?平面PAD,BM不在平面PAD内,∴BM∥平面PAD;
(2)以A为原点,AB,AD,AP分别为x,y,z轴,建立空间直角坐标系
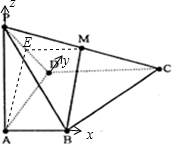
则B(1,0,0),C(2,2,0),D(0,2,0),P(0,0,2),M(1,1,1),E(0,1,1)
假设存在满足题意的点,则在平面PAD内,设N(0,y,z)
∴
=(-1,y-1,z-1),
=(1,0,-2),
=(1,-2,0)
由
•
=0,
•
=0,可得
,∴
∴N(0,
,
),∴N是AE的中点,此时MN⊥平面PBD;
(3)设直线PC与平面PBD所成的角为θ,则
=(2,2,-2),
=(-1,-
,-
),
设<
,
>为α,则cos<
,
>=
=
=-
∴sinθ=-cosα=
故直线PC与平面PBD所成角的正弦值为
•
所以四边形ABME为平行四边形,所以BM∥AE
又AE?平面PAD,BM不在平面PAD内,∴BM∥平面PAD;
(2)以A为原点,AB,AD,AP分别为x,y,z轴,建立空间直角坐标系

则B(1,0,0),C(2,2,0),D(0,2,0),P(0,0,2),M(1,1,1),E(0,1,1)
假设存在满足题意的点,则在平面PAD内,设N(0,y,z)
∴
| MN |
| PB |
| DB |
由
| MN |
| PB |
| MN |
| DB |
|
|
∴N(0,
| 1 |
| 2 |
| 1 |
| 2 |
(3)设直线PC与平面PBD所成的角为θ,则
| PC |
| MN |
| 1 |
| 2 |
| 1 |
| 2 |
设<
| PC |
| MN |
| PC |
| MN |
| ||||
|
|
| -2 | ||||||
2
|
| ||
| 3 |
∴sinθ=-cosα=
| ||
| 3 |
故直线PC与平面PBD所成角的正弦值为
| ||
| 3 |

练习册系列答案
相关题目



 +
+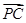 =
=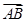 -
-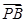 , 那么△PBC的面积与△ABC的面积之比是( )
, 那么△PBC的面积与△ABC的面积之比是( )