题目内容
在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=90°,D,E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ABD的重心G.则A1B与平面ABD所成角的余弦值( )

A.
| B.
| C.
| D.
|

连接BG,则BG是BE在面ABD上的所以,即∠EBG是AB与平面ABD所成的角,
设F为AB中点,连接EF、FG,
∵D、E分别是CC1、A1B的中点,又DC⊥平面ABC,
∴CDEF为矩形,
连接DF,G是△ADB的重心,
∴G∈DF,在直角三角形EFD中,EF2=FG•FD=
FD2,
设侧棱AA1=2a
∴EF=a,∴FD=
a
于是ED=
a,EG=
=
a,
∵FC=ED=
a,
∴AB=2
a,A1B=2
a,EB=
a.
∴sin∠EBG=
=
∴cos∠EBG=
∴直线A1B与平面ABD所成角的余弦值为
.
故选C.
设F为AB中点,连接EF、FG,
∵D、E分别是CC1、A1B的中点,又DC⊥平面ABC,
∴CDEF为矩形,
连接DF,G是△ADB的重心,
∴G∈DF,在直角三角形EFD中,EF2=FG•FD=
| 1 |
| 3 |

设侧棱AA1=2a
∴EF=a,∴FD=
| 3 |
于是ED=
| 2 |
1×
| ||
|
| ||
| 3 |
∵FC=ED=
| 2 |
∴AB=2
| 2 |
| 3 |
| 3 |
∴sin∠EBG=
| EG |
| EB |
| ||
| 3 |
∴cos∠EBG=
| ||
| 3 |
∴直线A1B与平面ABD所成角的余弦值为
| ||
| 3 |
故选C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



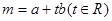 ,若
,若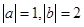 ,当且仅当
,当且仅当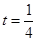 时,
时,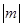 取得最小值,则向量a、b的夹角为___________.
取得最小值,则向量a、b的夹角为___________.