题目内容
16.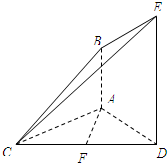 如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2AB,F是CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2AB,F是CD的中点.(1)求证:平面CBE⊥平面CDE;
(2)求直线EF与平面CBE所成角的正弦值.
分析 (1)由面面垂直的性质定理证明线面垂直,证得线线垂直,再证明面面垂直.
(2)过F作FN⊥CE交CE于N,则FN⊥平面CBE,连接EF,则∠NEF就是直线EF与平面CBE所成的角,找到角再利用线面关系求得,或者利用直角坐标系求解.
解答 (1)证明:因为DE⊥平面ACD,DE?平面CDE,所以平面CDE⊥平面ACD.
在底面ACD中,AF⊥CD,由面面垂直的性质定理知,AF⊥平面CDE.取CE的中点M,
连接BM、FM,由已知可得FM=AB且FM∥AB,则四边形FMBA为平行四边形,
从而BM∥AF.
所以BM⊥平面CDE.
又BM?平面BCE,则平面CBE⊥平面CDE.…(7分)
(2)法一:过F作FN⊥CE交CE于N,则FN⊥平面CBE,连接EF,则∠NEF就是直线
EF与平面CBE所成的角…(11分)
设AB=1,则$FN=\sqrt{2},EF=\sqrt{5}$,在Rt△EFN中,$sin∠NFE=\frac{FN}{EF}=\frac{\frac{\sqrt{2}}{2}}{\sqrt{5}}=\frac{\sqrt{10}}{10}$.
故直线EF与平面CBE所成角的正弦值为$\frac{\sqrt{10}}{10}$.…(15分)
法二:以F为坐标原点,FD、FA、FM所在直线为x,y,z轴,建立空间直角坐标系,如图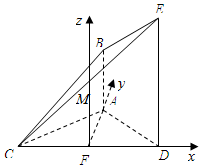
所示.F(0,0,0),E(1,0,2),$B(0,\sqrt{3},1)$,C(-1,0,0),平面CBE的一个法向量
为$\overrightarrow{n}=(-1,0,1),|\overrightarrow{n}|=\sqrt{2}$$\overrightarrow{EF}=(-1,0-2)$…(11分)
则 $cos<\overrightarrow{EF},\overrightarrow{n}>=\frac{|\overrightarrow{EF}•\overrightarrow{n}|}{|\overrightarrow{EF}||\overrightarrow{n}|}=\frac{1}{\sqrt{5}×\sqrt{2}}$=$\frac{\sqrt{10}}{10}$
故直线EF与平面CBE所成角的正弦值为$\frac{\sqrt{10}}{10}$.…(15分)
点评 本题主要考查了面面垂直的性质定理和线面教的求法,属于中档题型,高考常考.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案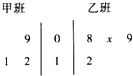 如图,茎叶图记录了某校甲班3名同学在一学年中去社会实践基地A实践的次数和乙班4名同学在同一学年中去社会实践基地B实践的次数.乙班记录中有一个数据模糊,无法确认,在图中用x表示.
如图,茎叶图记录了某校甲班3名同学在一学年中去社会实践基地A实践的次数和乙班4名同学在同一学年中去社会实践基地B实践的次数.乙班记录中有一个数据模糊,无法确认,在图中用x表示.