题目内容
4.若在曲线y=f(x)上以点A(x1,f(x1))为切点作切线l1,在曲线y=f(x)上总存在着以点B(x2,f(x2))为切点的切线l2(点B和点A不重合),使得l1∥l2,则对称曲线y=f(x)具有“可平行性”.已知f(x)=$\frac{1}{x}$+(a+$\frac{1}{a}$)lnx-x,其中a>0.(1)当a=2时,求y=f(x)在点(1,f(1))的切线方程;
(2)求函数y=f(x)在区间(0,1)上的极值;
(3)当a∈[3,+∞)时,函数y=f(x)具有“可平行性”,求x1+x2的范围.
分析 (1)欲求出切线方程,只须求出其斜率即可,故先利用导数求出在x=1处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决;
(2)求导数,再进行类讨论,利用导数的正负,确定函数的单调性,继而确定函数的极值;
(3)函数y=f(x)具有“可平行性”,意味着导数值相等,由此作为解题的突破口即可.
解答 解:(1)当a=2时,f(x)=$\frac{1}{x}$+$\frac{5}{2}$lnx-x,
∴f′(x)=-$\frac{1}{{x}^{2}}$+$\frac{5}{2x}$-1,
∴f′(1)=-1+$\frac{5}{2}$-1=$\frac{1}{2}$,f(1)=1+0-1=0,
∴y=f(x)在点(1,f(1))的切线方程为y=$\frac{1}{2}$(x-1),即x-2y-1=0;
(2)∵f(x)=$\frac{1}{x}$+(a+$\frac{1}{a}$)lnx-x,0<x<1,
∴f′(x)=-$\frac{1}{{x}^{2}}$+(a+$\frac{1}{a}$)$•\frac{1}{x}$-1=-$\frac{(x-a)(x-\frac{1}{a})}{{x}^{2}}$
令f′(x)=0,
解得x=a,或x=$\frac{1}{a}$
①当0<a<1时,则$\frac{1}{a}$>1,$\frac{1}{a}>a$,
当f′(x)<0,即x∈(0,a),f(x)在(0,a)单调递减,
当f′(x)>0,即(a,1)时,f(x)在(a,1)单调递增,
∴当x=a时,函数有极小值,极小值为f(a)=$\frac{1}{a}$+(a+$\frac{1}{a}$)lna-a,无极大值,
②当a=1时,$\frac{1}{m}$=1则,故x∈(0,1),f′(x)<0恒成立,
∴f(x)在(0,1)上单调递减,
此时,函数f(x)在(0,1)上无极值;
③当a>1时,0<$\frac{1}{a}$<1,
当f′(x)<0,即x∈(0,$\frac{1}{a}$),f(x)在(0,$\frac{1}{a}$)单调递减,
当f′(x)>0,即($\frac{1}{a}$,1)时,f(x)在($\frac{1}{a}$,1)单调递增,
∴当x=$\frac{1}{a}$时,函数有极小值,极小值为f($\frac{1}{a}$)=a-(a+$\frac{1}{a}$)lna-$\frac{1}{a}$,无极大值;
(3)∵当a∈[3,+∞)时,函数y=f(x)具有“可平行性”,
∴f′(x1)=f′(x2),(x1,x2>0,且x1≠x2)
即-$\frac{1}{{{x}_{1}}^{2}}$+(a+$\frac{1}{a}$)$\frac{1}{{x}_{1}}$-1=-$\frac{1}{{{x}_{2}}^{2}}$+(a+$\frac{1}{a}$)$\frac{1}{{x}_{2}}$-1,
∴x1+x2=(a+$\frac{1}{a}$)x1•x2,
∵x1≠x2,由不等式性质可得x1•x2<$(\frac{{x}_{1}+{x}_{2}}{2})^{2}$恒成立,
又x1,x2,a≥3,
∴x1+x2<(a+$\frac{1}{a}$)$(\frac{{x}_{1}+{x}_{2}}{2})^{2}$,
即x1+x2>$\frac{4}{a+\frac{1}{a}}$对a∈[3,+∞)恒成立,
令g(a)=a+$\frac{1}{a}$(a≥3),
则g′(a)=1-$\frac{1}{{a}^{2}}$>0恒成立
∴g(a)在[3,+∞)上单调递增,
∴g(a)min=g(3)=$\frac{10}{3}$,
∴$\frac{4}{a+\frac{1}{a}}$≤$\frac{4}{\frac{10}{3}}$=$\frac{6}{5}$,
∴x1+x2>$\frac{6}{5}$,
故x1+x2的范围为($\frac{6}{5}$,+∞)
点评 本小题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程,切线斜率和导数的关系是解决本题的关键.属于难题.

| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
 某几何体的三视图如图所示,则该几何体的体积为( )(单位cm3).
某几何体的三视图如图所示,则该几何体的体积为( )(单位cm3).| A. | $\frac{7}{12}π$ | B. | $\frac{7π}{3}$ | C. | $2\sqrt{2}π$ | D. | 3π |
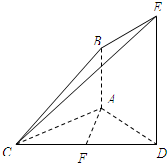 如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2AB,F是CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2AB,F是CD的中点.