题目内容
11.已知矩阵A=$[{\begin{array}{l}{\frac{3}{2}}&{\frac{1}{2}}\\ 2&1\end{array}}]$(1)求A-1;
(2)满足AX=A-1二阶矩阵X.
分析 (1)通过变换计算即可;
(2)通过AX=A-1可得X=A-1A-1,计算即可.
解答 解:(1)∵A=$[{\begin{array}{l}{\frac{3}{2}}&{\frac{1}{2}}\\ 2&1\end{array}}]$,
∴$[\begin{array}{l}{\frac{3}{2}}&{\frac{1}{2}}&{1}&{0}\\{2}&{1}&{0}&{1}\end{array}]$$\stackrel{第一行×2}{→}$$[\begin{array}{l}{3}&{1}&{2}&{0}\\{2}&{1}&{0}&{1}\end{array}]$$\stackrel{第二行+第一行×(-\frac{2}{3})}{→}$$[\begin{array}{l}{3}&{1}&{2}&{0}\\{0}&{\frac{1}{3}}&{-\frac{4}{3}}&{1}\end{array}]$$\stackrel{第二行×3}{→}$
$[\begin{array}{l}{3}&{1}&{2}&{0}\\{0}&{1}&{-4}&{3}\end{array}]$$\stackrel{第一行×\frac{1}{3}}{→}$$[\begin{array}{l}{1}&{\frac{1}{3}}&{\frac{2}{3}}&{0}\\{0}&{1}&{-4}&{3}\end{array}]$$\stackrel{第一行+第二行×(-\frac{1}{3})}{→}$$[\begin{array}{l}{1}&{0}&{2}&{-1}\\{0}&{1}&{-4}&{3}\end{array}]$,
∴A-1=$[\begin{array}{l}{2}&{-1}\\{-4}&{3}\end{array}]$;
(2)∵AX=A-1,∴X=A-1A-1=$[\begin{array}{l}{2}&{-1}\\{-4}&{3}\end{array}]$$[\begin{array}{l}{2}&{-1}\\{-4}&{3}\end{array}]$=$[\begin{array}{l}{8}&{-5}\\{-20}&{13}\end{array}]$,
即$X=[{\begin{array}{l}8&{-5}\\{-20}&{13}\end{array}}]$.
点评 本题考查矩阵乘法,注意解题方法的积累,属于基础题.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案| A. | $\sqrt{2}$ | B. | $\frac{{\sqrt{17}}}{3}$ | C. | $\frac{{2\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{33}}}{3}$ |
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
 在四棱锥P-ABCD中,PA⊥平面ABCD,E是PD的中点,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,AC=AP=2.
在四棱锥P-ABCD中,PA⊥平面ABCD,E是PD的中点,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,AC=AP=2. 如图,已知AB是⊙O的一条弦,AC是⊙O的直径,点P为AB延长线上一点,且PC为⊙O的一条切线,若AO=$\sqrt{2}$,PB=2,则PC的长是$2\sqrt{2}$.
如图,已知AB是⊙O的一条弦,AC是⊙O的直径,点P为AB延长线上一点,且PC为⊙O的一条切线,若AO=$\sqrt{2}$,PB=2,则PC的长是$2\sqrt{2}$.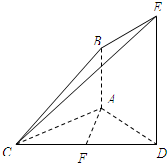 如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2AB,F是CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2AB,F是CD的中点.