题目内容
4.已知函数f(x)=ex-2ax,其中a∈R,e=2.71828…为自然对数的底数.(Ⅰ)求函数f(x)在区间[0,1]上的最小值;
(Ⅱ)证明:当x>0时,x2<ex;
(Ⅲ)证明:对任意给定的正数b,总存在x0,使得当x∈(x0,+∞),恒有x2<bex.
分析 (Ⅰ)f(x)=ex-2ax,f′(x)=ex-2a,对a分类讨论:当a≤$\frac{1}{2}$时,f′(x)≥0;当a≥$\frac{1}{2}$e时,f′(x)≤0;当$\frac{1}{2}<a<\frac{1}{2}e$时,令f′(x)=0,解得x=ln(2a),分别研究函数的单调性即可得出.
(Ⅱ)令g(x)=ex-x2,则g′(x)=ex-2x.由(I)得g′(x)≥2-2ln2>0,即可证明.
(III)方法一:①若b≥1,则ex≤bex.又由(II)知,当x>0时,x2<ex,即可证明;
②若0<b<1,令$k=\frac{1}{b}>1$,要使不等式x2<bex成立,只要ex>kx2成立.
而要使ex>kx2成立,则只要x>ln(kx2),即x>2lnx+lnk成立.令h(x)=x-2lnx-lnk,利用导数研究其单调性即可证明.
或用下列方式.②若0<b<1,则$\frac{1}{b}>1$,要使不等式x2<bex成立,则只要ln(x2)<lnbex,即2lnx<x+lnb成立.令h(x)=x-2lnx+lnb,利用导数研究其单调性即可证明.
方法二:对任意给定的正数b,取${x_o}=\frac{4}{{\sqrt{b}}}$.由(II)知,当x>0时,ex>x2,当x>xo时,ex$>(\frac{x}{2})^{2}(\frac{x}{2})^{2}$>$\frac{4}{b}(\frac{x}{2})^{2}$,即可证明.
解答 (Ⅰ)解:f(x)=ex-2ax,f′(x)=ex-2a,∵x∈[0,1],∴ex∈[1,e].
①当a≤$\frac{1}{2}$时,f′(x)=ex-2a≥0,∴函数f(x)在区间[0,1]上单调递增,f(x)≥f(0)=1,此时函数f(x)在区间[0,1]上的最小值为1.
②当a≥$\frac{1}{2}$e时,由f′(x)=ex-2a≤0,函数f(x)在区间[0,1]上单调递减,∴当x=1时,函数f(x)取得最小值,f(1)=e-2a.
③当$\frac{1}{2}<a<\frac{1}{2}e$时,令f′(x)=0,解得x=ln(2a),
当0<x<ln2a时,f′(x)<0,此时函数f(x)单调递减;当ln2a≤x≤1时,f′(x)≥0,此时函数f(x)单调递增.∴f(x)≥f(ln2a)=2a-2aln2a.
综上可知:当$a<\frac{1}{2}$时,f(x)的最小值为1;
当$\frac{1}{2}≤a≤\frac{e}{2}$时,f(x)的最小值为2a-2aln2a;
当$a>\frac{1}{2}e$时,f(x)的最小值为e-2a.
(Ⅱ)证明:令g(x)=ex-x2,则g′(x)=ex-2x.
由(I)得g′(x)≥2-2ln2>0,
故g(x)在R上单调递增,又g(0)=1>0,
因此,当x>0时,g(x)>g(0)>0,即x2<ex.
(III)①若b≥1,则ex≤bex.
又由(II)知,当x>0时,x2<ex.∴当x>0时,x2<bex.取x0=0,当x∈(x0,+∞)时,恒有x2<bx2.
②若0<b<1,令$k=\frac{1}{b}>1$,要使不等式x2<bex成立,只要ex>kx2成立.
而要使ex>kx2成立,则只要x>ln(kx2),即x>2lnx+lnk成立.
令h(x)=x-2lnx-lnk,则$h'(x)=1-\frac{2}{x}=\frac{x-2}{x}$.
∴所以当x>2时,h'(x)>0,h(x)在(2,+∞)内单调递增.
取x0=16k>16,所以h(x)在(x0,+∞)内单调递增.
又h(x0)=16k-2ln(16k)-lnk=8(k-ln2)+3(k-lnk)+5k.易知k>lnk,k>ln2,5k>0.所以h(x0)>0.即存在${x_0}=\frac{16}{b}$,当x∈(x0,+∞)时,恒有x2<bex.
综上,对任意给定的正数b,总存在x0,当x∈(x0,+∞)时,恒有x2<bex.
或用下列方式:
②若0<b<1,则$\frac{1}{b}>1$,
要使不等式x2<bex成立,则只要ln(x2)<lnbex,即2lnx<x+lnb成立.
令h(x)=x-2lnx+lnb,则$h'(x)=1-\frac{2}{x}=\frac{x-2}{x}$.
∴当x>2时,h′(x)>0,h(x)在(2,+∞)内单调递增.
取${x_0}=\frac{16}{b}>16$,∴h(x)在(x0,+∞)内单调递增.
又$h({x_0})=\frac{16}{b}-2ln(\frac{16}{b})+lnb=8(\frac{1}{b}-ln2)+3(\frac{1}{b}+lnb)+\frac{5}{b}$.
易知$\frac{1}{b}>ln\frac{1}{b},\frac{1}{b}>1>ln2,\frac{5}{b}>0$.∴h(x0)>0.
即存在${x_0}=\frac{16}{b}$,当x∈(x0,+∞)时,恒有x2<bex.
综上,对任意给定的正数b,总存在x0,当x∈(x0,+∞)时,恒有x2<bex.
方法二:对任意给定的正数b,取${x_o}=\frac{4}{{\sqrt{b}}}$
由(II)知,当x>0时,ex>x2,
∴${e^x}={e^{\frac{x}{2}}}•{e^{\frac{x}{2}}}>{(\frac{x}{2})^2}{(\frac{x}{2})^2}$,
当x>xo时,ex$>(\frac{x}{2})^{2}(\frac{x}{2})^{2}$>$\frac{4}{b}(\frac{x}{2})^{2}$=$\frac{1}{b}$x2.
因此,对任意给定的正数b,总存在x0,当x∈(x0,+∞)时,恒有x2<bex.
点评 本题考查了利用导数研究函数的单调性极值、利用已经证明的结论解决问题,考查了分类讨论思想方法、推理能力与计算能力,属于难题.

 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案| A. | 6 | B. | -6 | C. | $\frac{8}{3}$ | D. | -$\frac{8}{3}$ |
| A. | a>b>c | B. | c>a>b | C. | a>c>b | D. | c>b>a |
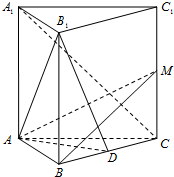 在正三棱柱ABC-A1B1C1中,点D是BC的中点.
在正三棱柱ABC-A1B1C1中,点D是BC的中点.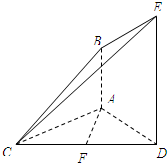 如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2AB,F是CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2AB,F是CD的中点.