题目内容
3.已知函数f(x)=(a-$\frac{1}{2}$)e2x+x(a∈R)(1)求f(x)在(0,+∞)上的单调区间;
(2)若f(x)<2aex在x∈(0,+∞)上恒成立,求实数a的取值范围.
分析 (1)f′(x)=(2a-1)e2x+1.e2x>1.对a分类讨论:当a≥$\frac{1}{2}$时,当0<a<$\frac{1}{2}$时,当a≤0时,利用导数研究函数的单调性即可得出.
(2)f(x)<2aex在x∈(0,+∞)上恒成立,?(2a-1)e2x-4aex+2x<0在x∈(0,+∞)上恒成立.令g(x)=(2a-1)e2x-4aex+2x,g′(x)=2[(2a-1)ex-1](ex-1).ex-1>0.对a分类讨论:①当a$≤\frac{1}{2}$时,再分类讨论:当$a<-\frac{1}{2}$时,当$-\frac{1}{2}≤a≤\frac{1}{2}$时,②当a$>\frac{1}{2}$时,利用导数研究函数的单调性极值即可得出.
解答 解:(1)f′(x)=(2a-1)e2x+1.e2x>1.
①当a≥$\frac{1}{2}$时,f′(x)>0,f(x)在(0,+∞)上的单调递增;
②当0<a<$\frac{1}{2}$时,$\frac{1}{1-2a}>$1,f′(x)=(2a-1)$({e}^{2x}-\frac{1}{1-2a})$,
令f′(x)=0,解得x0=$\frac{1}{2}ln\frac{1}{1-2a}$=-$\frac{1}{2}ln(1-2a)$.当x∈(0,x0)时,f′(x)>0,此时函数f(x)单调递增;
当x∈(x0,+∞)时,f′(x)<0,此时函数f(x)单调递减;
③当a≤0时,$0<\frac{1}{1-2a}≤1$,f′(x)=(2a-1)$({e}^{2x}-\frac{1}{1-2a})$<0,函数f(x)在(0,+∞)上的单调递减.
综上可得:当a≥$\frac{1}{2}$时,f(x)在(0,+∞)上的单调递增;
当0<a<$\frac{1}{2}$时,x0=-$\frac{1}{2}ln(1-2a)$.当x∈(0,x0)时,函数f(x)单调递增;当x∈(x0,+∞)时,函数f(x)单调递减;
当a≤0时,函数f(x)在(0,+∞)上的单调递减.
(2)f(x)<2aex在x∈(0,+∞)上恒成立,?(2a-1)e2x-4aex+2x<0在x∈(0,+∞)上恒成立.
令g(x)=(2a-1)e2x-4aex+2x,g′(x)=2[(2a-1)ex-1](ex-1).ex-1>0.
①当a$≤\frac{1}{2}$时,g′(x)<0,函数g(x)在x∈(0,+∞)上单调递减,g(x)<g(0)=-2a-1,
当$a<-\frac{1}{2}$时,g(0)>0,舍去;当$-\frac{1}{2}≤a≤\frac{1}{2}$时,g(0)≤0,满足条件.
②当a$>\frac{1}{2}$时,令g′(x)=0,解得x0=$\frac{1}{2a-1}$,当x∈(0,x0)时,函数f(x)单调递减;当x∈(x0,+∞)时,函数f(x)单调递增,且当x→+∞时,g(x)→+∞,不满足条件,舍去.
综上可得:实数a的取值范围是$[-\frac{1}{2},\frac{1}{2}]$.
点评 本题考查了利用导数研究函数的单调性极值、恒成立问题的等价转化方法,考查了分类讨论思想方法、推理能力与计算能力,属于难题.

| A. | 6 | B. | -6 | C. | $\frac{8}{3}$ | D. | -$\frac{8}{3}$ |
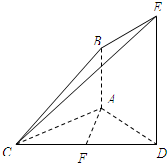 如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2AB,F是CD的中点.
如图,已知AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2AB,F是CD的中点.