题目内容
【题目】设数列{an}的前n项和为Sn , a1=10,an+1=9Sn+10.
(1)求证:{lgan}是等差数列;
(2)设Tn是数列{ ![]() }的前n项和,求Tn;
}的前n项和,求Tn;
(3)求使Tn> ![]() (m2﹣5m)对所有的n∈N*恒成立的整数m的取值集合.
(m2﹣5m)对所有的n∈N*恒成立的整数m的取值集合.
【答案】
(1)解:∵a1=10,an+1=9Sn+10.
∴当n=1时,a2=9a1+10=100,
故 ![]() ,
,
当n≥1时,an+1=9Sn+10 ①,
an+2=9Sn+1+10 ②,
两式相减得an+2﹣an+1=9an+1,
即an+2=10an+1,
即 ![]() ,
,
即{an}是首项a1=10,公比q=10的等比数列,
则数列{an}的通项公式 ![]() ;
;
则lgan=lg10n=n,
则lgan﹣lgan﹣1=n﹣(n﹣1)=1,为常数,
即{lgan}是等差数列;
(2)解:∵lgan=n,则 ![]() =
= ![]() (
( ![]() ﹣
﹣ ![]() ),
),
则Tn=3(1﹣ ![]() +…+
+…+ ![]() ﹣
﹣ ![]() )=3(1﹣
)=3(1﹣ ![]() )=3﹣
)=3﹣ ![]() ,
,
(3)解:∵Tn=3﹣ ![]() ≥T1=
≥T1= ![]() ,
,
∴要使Tn> ![]() (m2﹣5m)对所有的n∈N*恒成立,
(m2﹣5m)对所有的n∈N*恒成立,
则 ![]() >
> ![]() (m2﹣5m)对所有的n∈N*恒成立,
(m2﹣5m)对所有的n∈N*恒成立,
解得﹣1<m<6,
故整数m的取值集合{0,1,2,3,4,5}.
【解析】(1)根据等差数列的定义即可证明{lgan}是等差数列;(2)求出{ ![]() }的通项公式,利用裂项法即可求Tn;(3)直接解不等式即可得到结论.
}的通项公式,利用裂项法即可求Tn;(3)直接解不等式即可得到结论.
【考点精析】解答此题的关键在于理解等差关系的确定的相关知识,掌握如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,即![]() -
-![]() =d ,(n≥2,n∈N
=d ,(n≥2,n∈N![]()
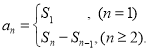 .
.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案【题目】某经销商从外地水产养殖厂购进一批小龙虾,并随机抽取40只进行统计,按重量分类统计结果如下图:

(1)记事件![]() 为:“从这批小龙虾中任取一只,重量不超过35
为:“从这批小龙虾中任取一只,重量不超过35![]() 的小龙虾”,求
的小龙虾”,求![]() 的估计值;
的估计值;
(2)若购进这批小龙虾100千克,试估计这批小龙虾的数量;
(3)为适应市场需求,了解这批小龙虾的口感,该经销商将这40只小龙虾分成三个等级,如下表:
等级 | 一等品 | 二等品 | 三等品 |
重量( |
|
|
|
按分层抽样抽取10只,再随机抽取3只品尝,记![]() 为抽到二等品的数量,求抽到二级品的期望.
为抽到二等品的数量,求抽到二级品的期望.
【题目】电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方
图:
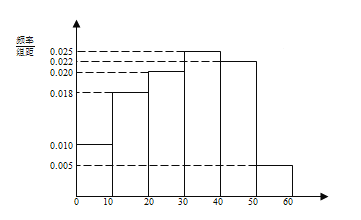
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.
(Ⅰ)根据已知条件完成下面的![]() 列联表,并据此资料,在犯错误的概率不超过
列联表,并据此资料,在犯错误的概率不超过![]() 的前提下,你是否有理由认为“体育迷”与性别有关?
的前提下,你是否有理由认为“体育迷”与性别有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
(Ⅱ)将上述调查所得到的频率视为概率,现在从该地区大量电视观众中,采用随机抽样方法每次抽取1名观众,抽取3次,记被抽取的3名观众中的“体育迷”人数为![]() .若每次抽取的结果是相互独立的,求
.若每次抽取的结果是相互独立的,求![]() 的分布列,期望
的分布列,期望![]() 和方差
和方差![]() .
.
附: 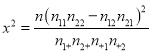
|
|
|
|
|
|