题目内容
【题目】已知圆M:x2+(y﹣4)2=4,点P是直线l:x﹣2y=0上的一动点,过点P作圆M的切线PA,PB,切点为A,B.
(1)当切线PA的长度为 ![]() 时,求点P的坐标;
时,求点P的坐标;
(2)若△PAM的外接圆为圆N,试问:当P在直线l上运动时,圆N是否过定点?若存在,求出所有的定点的坐标;若不存在,说明理由.
(3)求线段AB长度的最小值.
【答案】
(1)解:由题意知,圆M的半径r=2,M(0,4),设P(2b,b),
∵PA是圆M的一条切线,∴∠MAP=90°,
∴ ![]() ,解得
,解得 ![]() ,
,
∴P(0,0)或 ![]() .
.
(2)解:设P(2b,b),∵∠MAP=90°,∴经过A,P,M三点的圆N以MP为直径,
其方程为 ![]() ,
,
即(2x+y﹣4)b﹣(x2+y2﹣4y)=0,
由 ![]() ,解得
,解得 ![]() 或
或 ![]() ,
,
∴圆过定点(0,4), ![]() .
.
(3)解:因为圆N方程为 ![]() ,
,
即x2+y2﹣2bx﹣(b+4)y+4b=0,
圆M:x2+(y﹣4)2=4,即x2+y2﹣8y+12=0,
②﹣①得:圆M方程与圆N相交弦AB所在直线方程为:2bx+(b﹣4)y+12﹣4b=0,
点M到直线AB的距离 ![]() ,
,
相交弦长即: 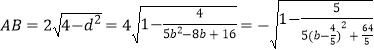 ,
,
当 ![]() 时,AB有最小值
时,AB有最小值 ![]() .
.
【解析】(1)根据圆M的标准方程即可求出半径r=2和圆心M坐标(0,4),并可设P(2b,b),从而由条件便可求出|MP|= ![]() ,这样便可求出b的值,即得出点P的坐标;(2)容易求出圆N的圆心坐标(b,
,这样便可求出b的值,即得出点P的坐标;(2)容易求出圆N的圆心坐标(b, ![]() ),及半径,从而可得出圆N的标准方程,化简后可得到(2x+y﹣4)b﹣(x2+y2﹣4y)=0,从而可建立关于x,y的方程,解出x,y,便可得出圆N所过的定点坐标;(3)可写出圆N和圆M的一般方程,联立这两个一般方程即可求出相交弦AB的直线方程,进而求出圆心M到直线AB的距离,从而求出弦长
),及半径,从而可得出圆N的标准方程,化简后可得到(2x+y﹣4)b﹣(x2+y2﹣4y)=0,从而可建立关于x,y的方程,解出x,y,便可得出圆N所过的定点坐标;(3)可写出圆N和圆M的一般方程,联立这两个一般方程即可求出相交弦AB的直线方程,进而求出圆心M到直线AB的距离,从而求出弦长 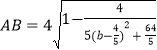 ,显然可看出b=
,显然可看出b= ![]() 时,AB取最小值,并求出该最小值.
时,AB取最小值,并求出该最小值.

 53随堂测系列答案
53随堂测系列答案【题目】高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
分组 | 频数 | 频率 |
[85,95) | ① | 0.025 |
[95,105) | 0.050 | |
[105,115) | 0.200 | |
[115,125) | 12 | 0.300 |
[125,135) | 0.275 | |
[135,145) | 4 | ② |
[145,155] | 0.050 | |
合计 | ③ |
(1)根据图表,①②③处的数值分别为、、;
(2)在所给的坐标系中画出[85,155]的频率分布直方图; 
(3)根据题中信息估计总体落在[125,155]中的概率.






