题目内容
1．过原点且倾斜角为60°的直线与圆x2+y2-4y=0相交，则圆的半径为2直线被圆截得的弦长为2$\sqrt{3}$．分析 先根据题意求得直线的方程，进而整理圆的方程求得圆心坐标和半径，进而利用点到直线的距离求得圆心到直线的距离，进而利用勾股定理求得弦长．
解答 解：过原点且倾斜角为60°的直线为y=$\sqrt{3}$x，
整理圆的方程为x2+（y-2）2=4，圆心为（0，2），半径r=2，
圆心到直线的距离为$\frac{|2+0|}{2}$=1，则弦长l=2$\sqrt{4-1}$=2$\sqrt{3}$．
故答案为：$2；2\sqrt{3}$．
点评 本题主要考查了直线与圆相交的性质．考查了基本的计算的能力和数形结合的思想的应用．
练习册系列答案
相关题目
11．已知函数f（x）的定义域是[-1，2]，则y=f（x）+f（-x）的定义域是（ ）
| A． | [-1，1] | B． | [-2，2] | C． | [-1，2] | D． | [-2，1] |
6．已知函数f（x）=$\frac{lnx}{x}$，则下列大小关系正确的是（ ）
| A． | f（e）＜f（3）＜f（2） | B． | f（e）＜f（2）＜f（3） | C． | f（2）＜f（3）＜f（e） | D． | f（3）＜f（2）＜f（e） |
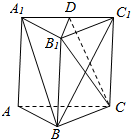如图所示，棱柱ABC-A1B1C1的侧面BCC1B1是菱形，设D是A1C1上的点且A1B∥平面B1CD，则A1D：DC1的值为1．
11．已知a，b，c三个数成等差数列，其中a=5+2$\sqrt{6}$，c=5-2$\sqrt{6}$，则b的值为（ ）
| A． | 2$\sqrt{6}$ | B． | $\sqrt{6}$ | C． | 5 | D． | 10 |