题目内容
12．函数f（x）=logax与g（x）=b-x其中a＞0，a≠1，ab=1）的图象可能是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 对a分类讨论，利用指数函数与对数函数的单调性即可得出．
解答 解：当a＞1时，则0＜b＜1，利用指数函数与对数函数的单调性可得：函数f（x）=logax与g（x）=b-x同为增函数，
当0＜a＜1时，则b＞1，利用指数函数与对数函数的单调性可得：函数f（x）=logax与g（x）=b-x同为减函数，
函数f（x）=logax与g（x）=b-x的单调性一致，
故选：C．
点评 本题考查了指数函数与对数函数的单调性，考查了分类讨论的思想方法，属于基础题．
练习册系列答案
相关题目
如图所示，在直四棱柱ABCD-A1B1C1D1中，DB=BC，DB⊥AC，点M是棱BB1上的一点．
7．直线y=-$\sqrt{3}$（x-2）截圆x2+y2=4所得的劣弧所对的圆心角为（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{π}{6}$ | C． | $\frac{2π}{3}$ | D． | $\frac{5π}{3}$ |
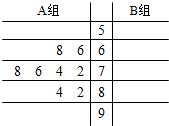某班A、B两组各有8名学生，他们期中考试的美术成绩如下：