题目内容
10.函数f(x)的定义域为D,若存在闭区间[a,b]⊆D,使得函数f(x)满足:①f(x)在[a,b]内是单调函数;②f(x)在[a,b]上的值域为[2a,2b],则称区间[a,b]为y=f(x)的“倍值区间”.下列函数中存在“倍值区间”的有①②④①f(x)=x2(x≥0);
②f(x)=2x(x∈R);
③f(x)=$\frac{4x}{{{x^2}+1}}$(x≥0);
④$f(x)={log_a}({a^x}-\frac{1}{8})(a>0,a≠1)$.
分析 利用“倍值区间”的意义,只要方程f(x)=2x在定义域内存在两个不同实数根即可得出.
解答 解:①假设函数f(x)存在“倍值区间”[a,b],由于x≥0,∴函数f(x)在[a,b]上单调递增,令x2=2x,解得x=0,2,∴[0,2]是函数f(x)的“倍值区间”;
同理可得:②存在“倍值区间”[1,2];③不存在“倍值区间”.
④假设函数f(x)存在“倍值区间”[a,b],令$lo{g}_{a}({a}^{x}-\frac{1}{8})$=2x,化为8(ax)2-8ax+1=0,∵△=64-32=32>0,解得ax=$\frac{2±\sqrt{2}}{4}$,因此x有两个不同的实数值满足方程.∴假设正确.
综上可得:只有①②④存在“倍值区间”.
故答案为:①②④.
点评 本题考查了系新定义“倍值区间”、方程的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
18.下列各组中的函数图象相同的是( )
| A. | f(x)=1,g(x)=x0 | B. | f(x)=1,g(x)=$\frac{x}{x}$ | ||
| C. | f(x)=$\frac{(x+3)^{2}}{x+3}$,g(x)=(x+3)(x+3)0 | D. | f(x)=|x|,g(x)=$\left\{\begin{array}{l}{x,x>0}\\{-x,x<0}\end{array}\right.$ |
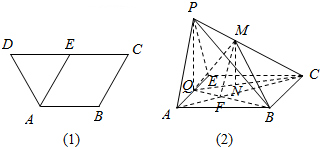 在等腰梯形ABCD中,AB∥CD,AB=BC=AD=2,CD=4,E为边DC的中点.如图1.将△ADE沿AE折起到△AEP位置,连PB、PC,点Q是棱AE的中点,点M在棱PC上,如图2.
在等腰梯形ABCD中,AB∥CD,AB=BC=AD=2,CD=4,E为边DC的中点.如图1.将△ADE沿AE折起到△AEP位置,连PB、PC,点Q是棱AE的中点,点M在棱PC上,如图2.