题目内容
已知点A(-2,0),B(1,0),平面内的动点P满足|PA|=λ|PB|(λ为常数,λ>0).
(1)求点P的轨迹E的方程,并指出其表示的曲线的形状.
(2)当λ=2时,P的轨迹E与x轴交于C、D两点,M是轨迹上异于C、D的任意一点,直线l:x=-3,直线CM与直线l交于点C′,直线DM与直线l交于点D'.求证:以C′D′为直径的圆总过定点,并求出定点坐标.
(1)求点P的轨迹E的方程,并指出其表示的曲线的形状.
(2)当λ=2时,P的轨迹E与x轴交于C、D两点,M是轨迹上异于C、D的任意一点,直线l:x=-3,直线CM与直线l交于点C′,直线DM与直线l交于点D'.求证:以C′D′为直径的圆总过定点,并求出定点坐标.
(1)设点P(x,y),由|PA|=λ|PB|得:
=λ
变形整理得:(1-λ2)x2+(1-λ2)y2+(4+2λ2)x+4-λ2=0
当λ=1时,化为x=-
,此时轨迹E所表示的曲线为直线.
当λ≠1时,化为(x+
)2+y2=
.
此时轨迹E所表示的曲线是以(-
,0)为圆心,半径为|
|的圆;
(2)λ=2时,方程(x+
)2+y2=
化为x2-4x+y2=0,
P的轨迹方程为x2-4x+y2=0,此时C(0,0)、D(4,0),设M(x0,y0),
则直线CM的方程为:y=
x.
联立方程
,得C′(-3,
),
直线DM的方程为:y=
(x-4).
联立方程
,D′(-3,
).
∴以C'D'为直径的圆的方程为(x+3)2+(y+
)(y+
)=0,
又
=4x0-
,整理得:(x+3)2+y2-21+
y=0.
令y=0,则有(x+3)2-21=0,解得x=-3±
∴以C'D'为直径的圆总过定点,且定点坐标为(-3±
,0).
| (x+2)2+y2 |
| (x-1)2+y2 |
变形整理得:(1-λ2)x2+(1-λ2)y2+(4+2λ2)x+4-λ2=0
当λ=1时,化为x=-
| 1 |
| 2 |
当λ≠1时,化为(x+
| λ2+2 |
| 1-λ2 |
| 9λ2 |
| (1-λ2)2 |
此时轨迹E所表示的曲线是以(-
| λ2+2 |
| 1-λ2 |
| 3λ |
| 1-λ2 |
(2)λ=2时,方程(x+
| λ2+2 |
| 1-λ2 |
| 9λ2 |
| (1-λ2)2 |
P的轨迹方程为x2-4x+y2=0,此时C(0,0)、D(4,0),设M(x0,y0),
则直线CM的方程为:y=
| y0 |
| x0 |
联立方程
|
| -3y0 |
| x0 |
直线DM的方程为:y=
| y0 |
| x0-4 |
联立方程
|
| -7y0 |
| x0-4 |
∴以C'D'为直径的圆的方程为(x+3)2+(y+
| 3y0 |
| x0 |
| 7y0 |
| x0-4 |
又
| y | 20 |
| x | 20 |
| 10x0-12 |
| y0 |
令y=0,则有(x+3)2-21=0,解得x=-3±
| 21 |
∴以C'D'为直径的圆总过定点,且定点坐标为(-3±
| 21 |

练习册系列答案
相关题目
 的离心率
的离心率 ,右焦点到直线
,右焦点到直线 1的距离
1的距离 ,O为坐标原点.
,O为坐标原点. 交于A、B两点,记△AOB的面积为S(O是坐标原点).
交于A、B两点,记△AOB的面积为S(O是坐标原点).
 ,
, 分别是椭圆
分别是椭圆 的左、右焦点,过
的左、右焦点,过 ,
, 两点,若
两点,若 ,
, ,则椭圆的离心率为( )
,则椭圆的离心率为( )
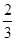


 +
+ =1的离心率,且e∈(
=1的离心率,且e∈( ,1),则实数k的取值范围是( )
,1),则实数k的取值范围是( ) )
)