题目内容
设等差数列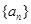 满足
满足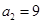 ,且
,且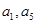 是方程
是方程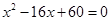 的两根。
的两根。
(1)求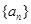 的通项公式;(2)求数列
的通项公式;(2)求数列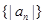 的前n项和
的前n项和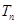 。
。
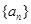 满足
满足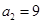 ,且
,且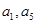 是方程
是方程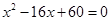 的两根。
的两根。(1)求
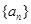 的通项公式;(2)求数列
的通项公式;(2)求数列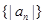 的前n项和
的前n项和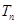 。
。(1) (2)
(2) 
 (2)
(2) 
试题分析:
(1)根据已知可得
 ,利用等差中项可得
,利用等差中项可得 ,所以根据已知可求出公差,进而求出首项,得通项公式.
,所以根据已知可求出公差,进而求出首项,得通项公式.(2)求和时需要清楚
 的正负,所以得分两种情况讨论.
的正负,所以得分两种情况讨论. 为正和负时分别求和.
为正和负时分别求和.试题解析:
(1)因为
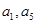 是方程
是方程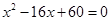 的两根,且它们是等差数列的两项,利用等差中项,有
的两根,且它们是等差数列的两项,利用等差中项,有 ,解得
,解得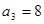 ,所以
,所以 ,所以
,所以 ,故根据等差数列的通项公式可得:
,故根据等差数列的通项公式可得: .
.(2)设等差数列
 的前n项和为
的前n项和为 ,所以
,所以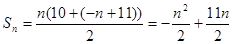 ,
, 由(1)可知,令
 ,解得
,解得 ,所以该数列的前11项是非负数项,从12项起为负数项.
,所以该数列的前11项是非负数项,从12项起为负数项.当
 时,
时, .
.当
 时,
时,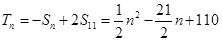 。
。综上所述,
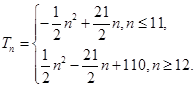

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 满足
满足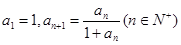
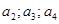 的值。
的值。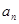 ,并用数学归纳法证明。
,并用数学归纳法证明。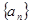 中,
中,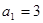 ,前n项和为
,前n项和为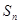
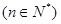 ,当
,当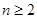 时,有
时,有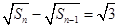 .(1)求数列
.(1)求数列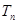 是数列
是数列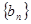 的前
的前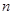 项和,若
项和,若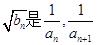 的等比中项,求
的等比中项,求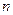 项和,若a1,a2,a5成等比数列,则S8="(" )
项和,若a1,a2,a5成等比数列,则S8="(" )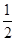
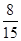
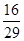
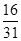
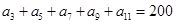 ,则
,则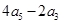 的值为( )
的值为( )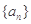 中,
中,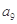 =
=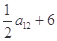 ,则数列
,则数列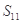 =( ).
=( ).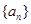 中,S10=120,则a1+a10等于 ( )
中,S10=120,则a1+a10等于 ( )