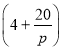Question

【题目】某高中三年级有AB两个班，各有50名同学，这两个班参加能力测试，成绩统计结果如表：

AB班成绩的频数分布表

分组	[50，60)	[60，70)	[70，80)	[80，90)	[90，100]
A班频数	4	8	23	9	6
B班频数	7	12	13	10	8

（1）试估计AB两个班的平均分；

（2）统计学中常用M值作为衡量总体水平的一种指标，已知M与分数t的关系式为：M.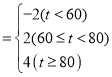

分别求这两个班学生成绩的M总值，并据此对这两个班的总体水平作简单评价.

Answer 1

【答案】(1)A=76，B=75 (2)见解析

【解析】

（1）取每组区间的中值作为该组的成绩，求出成绩总和，即可得出结论；

（2）分别统计出两个班在[50，60)，[60，80) ，[80，100]的人数，结合与分数的关系，即可求解.

(1)估计A班平均分为：

(4×55+8×65+23×75+9×85+6×95)=76，

B班平均分为：(7×55+12×65+13×75+10×85+8×95)=75.

(2)A班学生成绩的M总值为： MA=﹣2×4+2×(8+23)+4×(9+6)=114，

B班学生成绩的M总值为： MB=﹣2×7+2×(12+13)+4×(10+8)=108，

∵MA>MB，∴A班总体水平好于B班.