Question

【题目】某镇在政府“精准扶贫”的政策指引下，充分利用自身资源，大力发展养殖业，以增加收入，政府计划共投入72万元，全部用于甲、乙两个合作社，每个合作社至少要投入15万元，其中甲合作社养鱼，乙合作社养鸡，在对市场进行调研分析发现养鱼的收益M、养鸡的收益N与投入a（单位：万元）满足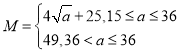，N＝a+20．设甲合作社的投入为x（单位：万元），两个合作社的总收益为f（x）（单位：万元）．

（1）当甲合作社的投入为25万元时，求两个合作社的总收益；

（2）试问如何安排甲、乙两个合作社的投入，才能使总收益最大，最大总收益为多少万元？

Answer 1

【答案】（1）88.5万元

（2）该公司在甲合作社投入16万元，在乙合作社投入56万元，总收益最大，最大总收益为89万元

【解析】

根据题意，当甲合作社投入为25万元时，乙合作社投入为47万元，分别代入其收益与投入的函数式，最后求和即可。

首先确定函数定义域，然后结合分段函数的解析式分类讨论确定最大收益的安排方法即可得出答案。

解：（1）当甲合作社投入为25万元时，乙合作社投入为47万元，此时两个个合作社的总收益为：

＝88.5（万元）；

（2）甲合作社的投入为x万元（15≤x≤57），则乙合作社的投入为72﹣x万元，

当15≤x≤36时，则36≤72﹣x≤57，

f（x）＝4+25+（72﹣x）+20＝﹣x+4+81．

令t＝，得≤t≤6，

则总收益为g（t）＝﹣t2+4t+81＝﹣（t﹣4）2+89，

显然当t＝4时，函数取得最大值g（t）＝89＝f（16），

即此时甲投入16万元，乙投入56万元时，总收益最大，最大收益为89万元

当36＜x≤57时，则15＜72﹣x≤36，

则f（x）＝49+（72﹣x）+20＝﹣x+105，

则f（x）在（36，57]上单调递减，

∴f（x）＜f（36）＝87．

即此时甲、乙总收益小于87万元．

又89＞87，

∴该公司在甲合作社投入16万元，在乙合作社投入56万元，总收益最大，最大总收益为89万元．