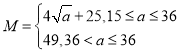题目内容
【题目】定义在
上的函数
，如果满足：对任意
，存在常数
，都有
成立，则称是上的有界函数，其中
称为函数的上界.已知函数
.
（1）当
时，求函数在
上的值域，并判断函数在上是否为有界函数，请说明理由；
（2）若是
上的有界函数，且的上界为3，求实数
的取值范围.
【答案】（1）值域为
，函数
在
上不是有界函数,详见解析（2）
【解析】
（1）利用函数的单调性得到函数的值域，从值域上观察不存在正数M，即函数在x∈（0，+∞）上不是有界函数．，
（2）根据函数f（x）在（﹣∞，0]上是以3为上界的函数，得到|1+2x+4x|≤3，换元以后得到关于t的不等式，根据二次函数的性质写出对称轴，求出a的范围．
（1）当
时，
，
因为在
上递增，所以
，
即在的值域为，故不存在常数
，使
成立，
所以函数在上不是有界函数.
（2）由已知函数f（x）在（﹣∞，0]上是以3为上界的函数，即：|1+a2x+4x|≤3
设t＝2x，所以t∈（0，1），不等式化为|1+at+t2|≤3
当0
时，1
且2+a≤3得﹣2<a＜0
当
或
时，即a≤﹣2或a≥0时，得﹣5≤a≤﹣2或0≤a≤1，
综上有.
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
