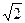题目内容
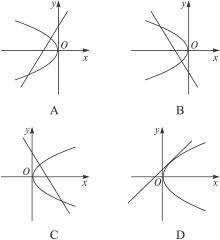
已知双曲线中心在原点,离心率为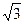
,若它的一条准线与抛物线y2=4x的准线重合,则该双曲线与抛物线交点到原点的距离是( )
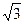,若它的一条准线与抛物线y2=4x的准线重合,则该双曲线与抛物线交点到原点的距离是( )A．2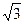+ 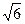| B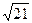． | C．18+12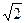 | D．21 |
B
抛物线的准线l:x=-1.对双曲线来说是其左准线,
∴-
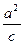=-1,
即a2=c.又离心率
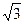=,联立解得a=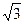,c=3,a2=3,b2=c2-a2=6,
∴双曲线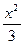
-
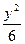=1,联立y2=4x,解得x=3且y=±2,
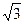即交点P(3,±2),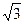
∴交点P到原点距离|OP|=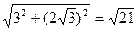
.
∴-
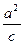=-1,即a2=c.又离心率
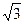=,联立解得a=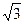,c=3,a2=3,b2=c2-a2=6,∴双曲线
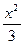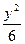-=1,联立y2=4x,解得x=3且y=±2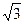,即交点P(3,±2
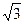),∴交点P到原点距离|OP|=
.
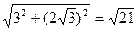练习册系列答案
相关题目
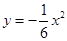的准线方程为 。
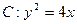，直线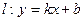
与C交于A，B两点，O为坐标原点。
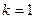，且直线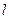
过抛物线C的焦点时，求
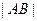的值；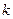
，
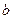之间满足的关系式，并证明直线
